Inflexiós pont

Az inflexiós pont (vagy hajlási pont) a függvénytanban, függvények analízisénél használt kifejezés, azt a pontot jelenti, ahol a függvénygörbe görbületet vált. A görbe alakja az inflexiós pontban változik konkávból konvexbe, vagy fordítva. A gyakorlati életben, ha az ember egy járművel hajtana végig a görbén, akkor egy pillanatig egyenes haladási irányba lenne állítva a kormány, miközben a jármű jobbról balra, vagy balról jobbra fordul.

Az f(x) = x³ függvény inflexiós pontja a (0,0)-ban van. Az x = 0 pontban a függvénynek nincs szélsőértéke, mert az f'(x) > 0 minden más pontban, tehát a függvény mindenütt szigorúan monoton növekvő

Az x³ + 2x² függvény inflexiós pontja, és az inflexiós pontban a függvényhez húzott érintő

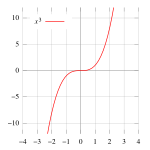
Az alábbi definíciók ekvivalensek:

• Ha az $f$ függvénynek $x_{0}$ pontban inflexiós pontja van, akkor az első deriváltjának $x_{0}$-ban szélsőértéke van: minimum vagy maximum (lehet csak helyi szélsőérték is)
• Az inflexiós pont az a pont a görbén, amelyben a második derivált előjelet vált (azaz az inflexiós pontban a második derivált függvényértéke nulla $f''(x_{0})=0$).
• A függvénygörbének az a pontja, amelybe ha érintőt húzunk, akkor az érintő egyenese átmetszi a függvényt az inflexiós pontban. Ezt könnyű belátni, ugyanis a konvex és konkáv része a grafikonnak csak az érintő különböző oldalán lehet.

Feltételek az inflexiós pont létezéséhez

Szükséges feltételek

• $f$ legyen az $x_{0}$ pont egy környezetében kétszer differenciálható
• $x_{0}$ az inflexiós pont,
  ekkor:

$f''(x_{0})=0\,$

Elégséges feltételek

• $f$ függvény második deriváltja előjelet vált $x_{0}$ pontban. Ha $f\,''(x)$ pozitívból negatívba vált az inflexiós pontban, akkor $f\,(x)$ konvexből konkávba vált, ha $f\,''(x)$ negatívból pozitívba vált, akkor pedig $f\,(x)$ konkávból konvexbe megy át.
• Legyen az $f$ függvény $x_{0}$ pont egy környezetében háromszor differenciálható. Ekkor ha $f\,''(x_{0})=0$ és $f'''(x_{0})\neq 0$, akkor $x_{0}$ inflexiós pont. Ha az $\,f'''>0$, akkor a függvénygörbe konkávból konvexbe, ha pedig $\,f'''<0$ akkor konvexből konkávba vált.

Az inflexiós pont egy speciális, magasabb dimenziókban előforduló fajtája a nyeregpont.

Amennyiben a függvény első deriváltja egy adott pontban szélsőértéket vesz fel, akkor abból következik, hogy abban a pontban a második derivált értéke nulla: $f''(x)=0$, de ez a feltétel (szükséges feltétel) önmagában még nem elegendő az inflexiós pont meglétéhez. Általánosan ennek megállapításához mindig szükség van a legutolsó még nem nulla deriváltfüggvény megvizsgálására.

Példa

${f(x)}={1 \over 3}\cdot x^{3}-2\cdot x^{2}+3\cdot x$

A függvény második deriváltja:

${f''(x)}={2\cdot x-4}$

Ekkor teljesülnie kell, hogy:

${f''(x)}=0={2\cdot x-4}$

Az eredmény $x=2$. (Itt lehet inflexiós pontja $f$-nek.)

Egyúttal

${f'''(x)}=2\,$

ami nem 0, azaz a függvénynek itt inflexiós pontja van.

Különleges esetek

• ${f(x)}=(x-2)\cdot e^{|x|}$
  Ennek a függvénynek a grafikonja görbületet vált az $x=0$ pontban konvexből konkávba. Ennek ellenére ez nem inflexiós pont, mivel itt az első derivált nem létezik, tehát szélsőértéke sem lehet.

• ${f(x)}=x\cdot |x|$
  Ennek a függvénynek az $x=0$ pontban inflexiós pontja van, bár a nem létezik az ${f''(0)}\,$. Ennek ellenére az első deriváltnak, ${f'}\,$-nek $x=0$-ban minimuma van.