Kiváló erősen összetett számok
A számelméletben a kiváló erősen összetett számok (superior highly composite number, SHCN) olyan pozitív egész számok, melyeknek a náluk kisebb számoknál több osztójuk van, egy bizonyos módon skálázva a számokat. Ez erősebb megkötés, mint az erősen összetett számoké, mely csak azt követeli meg, hogy több osztójuk legyen, mint bármely náluk kisebb számnak.
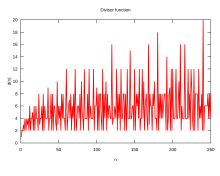
Az első 10 kiváló erősen összetett szám és prímtényezős felbontásuk:
| # prím- tényezők |
SHCN n |
prím- felbontás |
prím- kitevők |
# osztók d(n) |
primoriális felbontás | |
|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 1 | 2 | 2 | 2 |
| 2 | 6 | 2 ⋅ 3 | 1,1 | 22 | 4 | 6 |
| 3 | 12 | 22 ⋅ 3 | 2,1 | 3×2 | 6 | 2 ⋅ 6 |
| 4 | 60 | 22 ⋅ 3 ⋅ 5 | 2,1,1 | 3×22 | 12 | 2 ⋅ 30 |
| 5 | 120 | 23 ⋅ 3 ⋅ 5 | 3,1,1 | 4×22 | 16 | 22 ⋅ 30 |
| 6 | 360 | 23 ⋅ 32 ⋅ 5 | 3,2,1 | 4×3×2 | 24 | 2 ⋅ 6 ⋅ 30 |
| 7 | 2520 | 23 ⋅ 32 ⋅ 5 ⋅ 7 | 3,2,1,1 | 4×3×22 | 48 | 2 ⋅ 6 ⋅ 210 |
| 8 | 5040 | 24 ⋅ 32 ⋅ 5 ⋅ 7 | 4,2,1,1 | 5×3×22 | 60 | 22 ⋅ 6 ⋅ 210 |
| 9 | 55440 | 24 ⋅ 32 ⋅ 5 ⋅ 7 ⋅ 11 | 4,2,1,1,1 | 5×3×23 | 120 | 22 ⋅ 6 ⋅ 2310 |
| 10 | 720720 | 24 ⋅ 32 ⋅ 5 ⋅ 7 ⋅ 11 ⋅ 13 | 4,2,1,1,1,1 | 5×3×24 | 240 | 22 ⋅ 6 ⋅ 30030 |
Formális definíció szerint: n pozitív egész akkor kiválóan erősen összetett szám, ha létezik olyan pozitív ε valós szám, amire minden k természetes számra
- ,
ahol d(n) az osztószám-függvény, ami n osztóinak számát jelöli. A kifejezést Rámánudzsan használta először 1915-ben.
Az első 15 kiváló erősen összetett szám – 2, 6, 12, 60, 120, 360, 2520, 5040, 55440, 720720, 1441440, 4324320, 21621600, 367567200, 6983776800 (A002201 sorozat az OEIS-ben) – megegyezik az első 15 kolosszálisan bővelkedő számmal, melyek hasonló feltételnek tesznek eleget, de az osztóösszeg-függvény alapján.
Jegyzetek
szerkesztés- (1915) „Highly composite numbers”. Proc. London Math. Soc. (2) 14, 347-409. o. DOI:10.1112/plms/s2_14.1.347. Reprinted in Collected Papers (Ed. G. H. Hardy et al.), New York: Chelsea, pp. 78–129, 1962
- Handbook of number theory I. Dordrecht: Springer-Verlag, 45–46. o. (2006). ISBN 1-4020-4215-9
További információk
szerkesztés- Weisstein, Eric W.: Superior highly composite number (angol nyelven). Wolfram MathWorld
