Klikk (gráfelmélet)

A matematika, azon belül a gráfelmélet területén a klikk (clique) egy irányítatlan gráf csúcsainak olyan halmaza, melyek feszített részgráfja teljes; tehát a klikk bármely két csúcsa között van él, bármely két csúcsa szomszédos. A klikk a gráfelmélet alapvető fogalmai közé tartozik, számos matematikai problémában és gráfkonstrukcióban előkerülnek. A klikkeket a számítástudomány is behatóan tanulmányozta: annak eldöntése, hogy létezik-e egy gráfban adott méretű klikk (a klikkprobléma) NP-teljes; a probléma nehézsége ellenére számos, klikkek keresésére szolgáló algoritmus létezik.

Egy gráf, melynek van

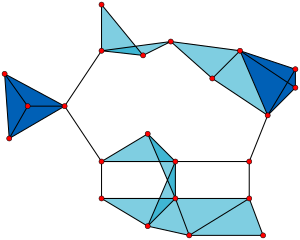
• 23 db 1 csúcsú klikkje (a csúcsok),
• 42 db 2 csúcsú klikkje (az élek),
• 19 db 3 csúcsú klikkje (a világosabb és sötétebb kék háromszögek) és
• 2 db 4 csúcsú klikkje (sötétkék területek).

A 11 világoskék háromszög maximális klikkeket alkot. A két sötétkék 4-klikk maximális, egyben maximális elemszámú is, továbbá a gráf klikkszáma is 4.

Egy biklikk: a K3,3 teljes páros gráf.

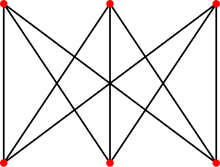
Bár a teljes részgráfok vizsgálata visszanyúlik legalább a Ramsey-elmélet (Erdős & Szekeres 1935) által elvégzett gráfelméleti átfogalmazásáig, magát a klikk kifejezést elsőként (Luce & Perry 1949) használta, aki az ismeretségi hálózatok teljes részgráfjaival modellezte az emberekből álló klikkeket; tehát olyan embercsoportokat, akik közül mindenki ismer mindenkit. A klikkek számos más tudományterületen ismertek, különösen a bioinformatikában.

Definíciók

Egy G = (V, E) irányítatlan gráf C klikkje csúcsainak olyan C ⊆ V részhalmaza, melyben bármely két csúcs szomszédos. Ezzel ekvivalens megfogalmazás, hogy a G gráf C által feszített részgráfja teljes gráf. Egyes esetekben a klikk kifejezés alatt magát a feszített részgráfot értjük.

A klikk csúcsainak számát a klikk méretének vagy rendjének is mondják. A k csúcsú klikket röviden k-klikknek is nevezik.

A maximális klikk (maximal clique) a gráf olyan klikkje, ami nem terjeszthető ki szomszédos csúcsok hozzáadásával, tehát csúcsai nem képezik egy másik klikk valódi részhalmazát. Egyes szerzők klikk-meghatározása eleve magában foglalja a maximalitás kritériumát, ők a nem maximális teljes részgráfokra más terminológiát alkalmaznak.

A maximális elemszámú klikk (maximum clique) a G gráfnak olyan klikkje, aminél nincsen több csúcsból álló klikk a gráfban.

A G gráf klikkszáma a maximális elemszámú klikkjének a mérete; a jele ω(G).

A G gráf metszetszáma (intersection number) a G éleit lefedő klikkek lehetséges minimális száma.

A G gráf klikkfedési száma (clique cover number) a G csúcsait lefedő (nem feltétlenül diszjunkt) klikkek lehetséges minimális száma.

A klikk „ellentéte” a független csúcshalmaz, abban az értelemben, hogy minden klikk a komplementer gráf egy független csúcshalmazának felel meg. A klikkfedési probléma a gráf csúcsait lefedő minimális számú klikk megkeresése.

Kapcsolódó fogalom a bi-klikk, páros klikk avagy teljes páros részgráf. Egy gráf biklikkfedési száma (bipartite dimension), d(G) a gráf éleit lefedő páros klikkek lehetséges minimális száma.

Egy gráf klikkgráfja az a gráf, aminek minden pontja megfelel az eredeti gráf egy-egy maximális klikkjének, és két pont akkor van összekötve, ha a megfelelő klikkek metszete nem üres.

Eredmények

A klikkekkel kapcsolatos matematikai eredmények közül néhány:

• Tetszőleges gráfra teljesül, hogy (az i-edik csúcs fokszámát d_i-vel jelölve)

$\omega (G)\geq \sum _{i=1}^{n}{\frac {1}{n-d_{i}}}$

• A legkisebb olyan R szám, amire egy R csúcsú gráfban biztosan van egy m csúcsú klikk vagy egy n elemű független ponthalmaz, az $R(m,n)$ Ramsey-szám. A Ramsey-tétel kimondja, hogy minden m-re és n-re létezik ilyen szám, de a pontos értékük meghatározása nehéz feladat.
• A klikkszám mindig kisebb vagy egyenlő, mint a kromatikus szám; azt a gráfot, aminek minden feszített részgráfjára teljesül, hogy a klikkszáma megegyezik a kromatikus számával, perfekt gráfnak nevezzük. A legnagyobb olyan n csúcsú gráf, amiben nincs k csúcsú klikk, a $T_{n,k}$ Turán-gráf.
• A Turán-tétel (Turán 1941) alsó korlátot ad a sűrű gráfok klikkjeinek méretére. Ha egy gráf elegendően sok éllel rendelkezik, tartalmaznia kell egy nagy klikket. Például minden, $n$ csúccsal és több mint $\scriptstyle \lfloor {\frac {n}{2}}\rfloor \cdot \lceil {\frac {n}{2}}\rceil$ éllel rendelkező gráfban kell lennie 3-klikknek.
• A Ramsey-tétel értelmében (Graham, Rothschild & Spencer 1990) bármely gráf vagy a komplementere legalább a csúcsok számának logaritmusa szerinti klikket tartalmaz.
• (Moon & Moser 1965) eredménye szerint egy 3n csúcsból álló gráf legfeljebb 3ⁿ maximális klikket tartalmazhat. A korlátot ténylegesen elérő gráfok a K_3,3,... Moon–Moser-gráfok , a Turán-tétel extremális eseteként fellépő Turán-gráfok speciális esetei.
• A Hadwiger-sejtés a gráf legnagyobb klikk minorját (a gráf Hadwiger-számát) a kromatikus számával hozza kapcsolatba.
• Az Erdős–Faber–Lovász-sejtés szintén a gráfok színezését hozza kapcsolatba a klikkekkel.

Számos fontos gráfosztály határozható meg vagy karakterizálható klikkjei alapján:

• Egy klasztergráf vagy P3-mentes gráf olyan gráf, melynek összefüggő komponensei klikkek.
• Egy blokkgráf vagy klikkfa olyan gráf, melyben minden kétszeresen összefüggő komponens klikk.
• Egy húrgráf olyan gráf, melynek csúcsaira létezik olyan rendezés, hogy bármely v csúcs környezetében lévő csúcsok közül a rendezésben utána következő csúcsok klikket alkotnak (bármely feszített részgráf tartalmaz szimpliciális csúcsot).
• Egy kográf olyan gráf, melynek feszített részgráfjaiban bármely maximális klikk bármely maximális független csúcshalmazt egyetlen csúcsban metsz.
• Egy intervallumgráf olyan gráf, melynek maximális klikkjeire létezik olyan rendezés, hogy bármely v csúcsra a v-t tartalmazó klikkek egymás után következnek a rendezésben.
• Egy élgráf olyan gráf, melyben lehetséges klikkek olyan éldiszjunkt gyűjteményét azonosítani (megengedve, hogy egyes klikkek egyetlen csúcsból álljanak), melyek a gráf éleit úgy particionálják, hogy a gráf minden csúcsa pontosan két klikkbe tartozzon.
• Egy perfekt gráf olyan gráf, melynek minden feszített részgráfjában a kromatikus szám a klikkszámmal megegyezik.
• Egy split gráf olyan gráf, melynek csúcsai egy klikkbe és egy független csúcshalmazba oszthatók szét.
• Egy háromszögmentes gráfban a csúcsokon és éleken kívül nincsen több klikk.

A fentieken túl számos más matematikai konstrukciónak van köze a klikkekhez. Néhány közülük:

• A G gráf klikk-komplexuma egy X(G) absztrakt szimpliciális komplexum, mely G minden klikkjéhez egy szimplexet tartalmaz.
• A G gráfhoz tartozó irányítatlan κ(G) szimplexgráf egy csúcsot tartalmaz G minden klikkjéhez és minden olyan klikk között húzódik él, melyek egyetlen csúcsban különböznek. A mediángráfok közé tartozik, és kapcsolódik a gráf klikkjeinek medián algebrájához: az A, B, és C klikken értelmezett m(A,B,C) medián egy olyan klikk, melynek csúcsai az A, B és C klikkek közül legalább kettőbe beletartoznak.
• A klikk-összeg művelet segítségével két gráf egy közös klikk mentén összefűzhető.
• A klikkszélesség egy gráf bonyolultságát fejezi ki annak fényében, hogy legalább hány különbözően címkézett csúcsra van szükség ahhoz, hogy a gráfot felépítsük a diszjunkt unió, átcímkézés és az adott címkéjű csúcspárok összekötésének művelete segítségével. Az 1 klikkszélességű gráfok éppen a diszjunkt klikkekből felépített gráfok (klasztergráfok).
• Egy gráf metszetszáma éleit lefedő klikkek lehetséges minimális száma.
• Egy gráf klikkgráfja a maximális klikkjei metszetgráfjának felel meg.

A teljes részgráfokkal közeli kapcsolatban álló fogalmak a teljes gráfok topologikusan izomorf felosztásai és a teljes gráfminorok. A Kuratowski-tétel és a Wagner-tétel a síkgráfokat tiltott teljes, illetve teljes páros felosztásaik és minoraik alapján karakterizálja.

Számítástudomány

A számítástudományban a klikkprobléma adott gráf maximális elemszámú klikkjének, illetve összes klikkjének megkeresése. NP-teljes, szerepel Karp 21 NP-teljes problémája között. Egyben rögzített paraméter mellett kezelhető és nehezen approximálható probléma. A klikkek keresésére kifejlesztett legjobb algoritmusok vagy exponenciális időben futnak (mint a Bron–Kerbosch-algoritmus) vagy valamely gráfosztályra vannak specializálva (pl. síkgráfok vagy perfekt gráfok), melyekre a probléma polinom időben megoldható.

Alkalmazásai

Maga a „klikk” kifejezés és gráfelméleti használata (Luce & Perry 1949) munkásságából ered, aki az ismeretségi hálózatok teljes részgráfjaival modellezte az emberekből álló klikkeket; tehát olyan embercsoportokat, akik közül mindenki ismer mindenkit. Az ismeretségi hálózatok gráfelméleti vizsgálatának további fejleményeihez lásd pl. (Alba 1973), (Peay 1974) és (Doreian & Woodard 1994).

A bioinformatika számos különböző problémáját modellezték klikkek segítségével. Például (Ben-Dor, Shamir & Yakhini 1999) a génkifejeződési adatok klaszterezésének problémáját úgy modellezi, mint egy gráf diszjunkt klikkek uniójává való átalakításához szükséges lépések minimális számát; (Tanay, Sharan & Shamir 2002) egy hasonló biklaszterezési problémát tárgyal, mely megköveteli, hogy minden klaszter egyben klikk legyen. (Sugihara 1984) a klikkek segítségével modellezi a táplálékláncok niche-eit. (Day & Sankoff 1986) filogenetikai fák (evolúciós leszármazási vonalak) kikövetkeztetésének problémáját úgy írja le, mint egy olyan gráf maximális elemszámú klikkjeinek megkeresését, melyben a csúcsok a fajok tulajdonságait jelentik, és két csúcs akkor szomszédos, ha a két tulajdonság tökéletesen (homoplázia nélküli törzsfejlődési vonallal) összeköthető. (Samudrala & Moult 1998) a fehérjeszerkezet-előrejelzést úgy modellezik, mint klikkek keresését egy olyan gráfban, melynek csúcsai a fehérjék alegységeinek elhelyezkedéseinek felelnek meg. És a fehérjék közötti kölcsönhatások hálózatában klikkek keresésével (Spirin & Mirny 2003) fehérjék olyan klaszterét találta meg, melyek egymással szorosan kölcsönhatnak, de a klaszteren kívül kevés fehérjével lépnek kölcsönhatásba. A power graph analysis nevű módszer egyszerűsíti a komplex biológiai hálózatokat azzal, hogy a klikkeket és hasonló struktúrákat tekinti a hálózat alapvető építőelemeinek.

A villamosmérnöki szakmában (Prihar 1956) a klikkek segítségével analizált távközlési hálózatokat, (Paull & Unger 1959) pedig részlegesen specifikált Boole-függvények számításával hatékony áramkörök tervezésére használta őket. Klikkeket alkalmaztak automatikus tesztmintázat-előállításra is: a lehetséges hibák ún. inkompatibilitási gráfjában lévő nagy klikk alsó korlátot ad a teszthalmaz méretére. (Cong & Smith 1993) leírja a klikkek egy alkalmazási területét egy elektronikus áramkör kisebb alegységekre való hierarchikus particionálásában.

A kémiában (Rhodes et al. 2003) egy kémiai adatbázisban klikkekkel jellemez olyan vegyi anyagokat, melyek a célul kitűzött térszerkezettel nagyfokú hasonlóságot mutatnak. (Kuhl, Crippen & Friesen 1983) klikkekkel modellezi két vegyi anyag egymással való kötőhelyeit.

Fordítás

• Ez a szócikk részben vagy egészben a Clique (graph_theory) című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

• Alba, Richard D. (1973), "A graph-theoretic definition of a sociometric clique", Journal of Mathematical Sociology 3 (1): 113–126, doi:10.1080/0022250X.1973.9989826, <http://aris.ss.uci.edu/~lin/1.pdf> Archiválva 2011. május 3-i dátummal a Wayback Machine-ben.
• Barthélemy, J.-P.; Leclerc, B. & Monjardet, B. (1986), "On the use of ordered sets in problems of comparison and consensus of classifications", Journal of Classification 3 (2): 187–224, DOI 10.1007/BF01894188.
• Ben-Dor, Amir; Shamir, Ron & Yakhini, Zohar (1999), "Clustering gene expression patterns.", Journal of Computational Biology 6 (3–4): 281–297, DOI 10.1089/106652799318274.
• Cong, J. & Smith, M. (1993), "A parallel bottom-up clustering algorithm with applications to circuit partitioning in VLSI design", Proc. 30th International Design Automation Conference, pp. 755–760, DOI 10.1145/157485.165119.
• Day, William H. E. & Sankoff, David (1986), "Computational complexity of inferring phylogenies by compatibility", Systematic Zoology 35 (2): 224–229, DOI 10.2307/2413432.
• Doreian, Patrick & Woodard, Katherine L. (1994), "Defining and locating cores and boundaries of social networks", Social Networks 16 (4): 267–293, DOI 10.1016/0378-8733(94)90013-2.
• Erdős, Paul & Szekeres, George (1935), "A combinatorial problem in geometry", Compositio Mathematica 2: 463–470, <http://www.renyi.hu/~p_erdos/1935-01.pdf>.
• Graham, R.; Rothschild, B. & Spencer, J. H. (1990), Ramsey Theory, New York: John Wiley and Sons, ISBN 0-471-50046-1.
• Hamzaoglu, I. & Patel, J. H. (1998), "Test set compaction algorithms for combinational circuits", Proc. 1998 IEEE/ACM International Conference on Computer-Aided Design, pp. 283–289, DOI 10.1145/288548.288615.
• Karp, Richard M. (1972), "Reducibility among combinatorial problems", in Miller, R. E. & Thatcher, J. W., Complexity of Computer Computations, New York: Plenum, pp. 85–103, <http://www.cs.berkeley.edu/~luca/cs172/karp.pdf>. Hozzáférés ideje: 2017-03-03 Archiválva 2011. június 29-i dátummal a Wayback Machine-ben.
• Kuhl, F. S.; Crippen, G. M. & Friesen, D. K. (1983), "A combinatorial algorithm for calculating ligand binding", Journal of Computational Chemistry 5 (1): 24–34, DOI 10.1002/jcc.540050105.
• Kuratowski, Kazimierz (1930), "Sur le probléme des courbes gauches en Topologie", Fundamenta Mathematicae 15: 271–283, <http://matwbn.icm.edu.pl/ksiazki/fm/fm15/fm15126.pdf>.
• Luce, R. Duncan & Perry, Albert D. (1949), "A method of matrix analysis of group structure", Psychometrika 14 (2): 95–116, DOI 10.1007/BF02289146.
• Moon, J. W. & Moser, L. (1965), "On cliques in graphs", Israel J. Math. 3: 23–28, DOI 10.1007/BF02760024.
• Paull, M. C. & Unger, S. H. (1959), "Minimizing the number of states in incompletely specified sequential switching functions", IRE Trans. on Electronic Computers EC-8 (3): 356–367, DOI 10.1109/TEC.1959.5222697.
• Peay, Edmund R. (1974), "Hierarchical clique structures", Sociometry 37 (1): 54–65, DOI 10.2307/2786466.
• Prihar, Z. (1956), "Topological properties of telecommunications networks", Proceedings of the IRE 44 (7): 927–933, DOI 10.1109/JRPROC.1956.275149.
• Rhodes, Nicholas; Willett, Peter & Calvet, Alain et al. (2003), "CLIP: similarity searching of 3D databases using clique detection", Journal of Chemical Information and Computer Sciences 43 (2): 443–448, DOI 10.1021/ci025605o.
• Samudrala, Ram & Moult, John (1998), "A graph-theoretic algorithm for comparative modeling of protein structure", Journal of Molecular Biology 279 (1): 287–302, DOI 10.1006/jmbi.1998.1689.
• Spirin, Victor & Mirny, Leonid A. (2003), "Protein complexes and functional modules in molecular networks", Proceedings of the National Academy of Sciences 100 (21): 12123–12128, DOI 10.1073/pnas.2032324100.
• Sugihara, George (1984), "Graph theory, homology and food webs", in Levin, Simon A., Population Biology, vol. 30, Proc. Symp. Appl. Math., pp. 83–101.
• Tanay, Amos; Sharan, Roded & Shamir, Ron (2002), "Discovering statistically significant biclusters in gene expression data", Bioinformatics 18 (Suppl. 1): S136–S144, DOI 10.1093/bioinformatics/18.suppl_1.S136.
• Turán, Paul (1941), "On an extremal problem in graph theory", Matematikai és Fizikai Lapok 48: 436–452

További információk

• Weisstein, Eric W.: Clique (angol nyelven). Wolfram MathWorld
• Weisstein, Eric W.: Clique Number (angol nyelven). Wolfram MathWorld