Koch-görbe

A Koch-görbe vagy Koch-hópehely Helge von Koch svéd matematikus által 1904-ben leírt fraktál, mely ilyen minőségében az egyik legelső.

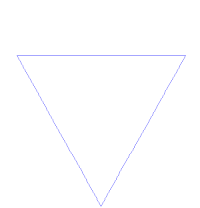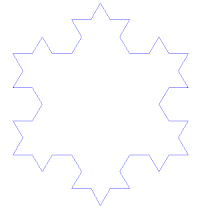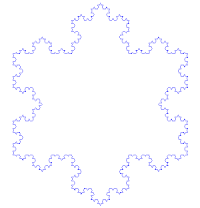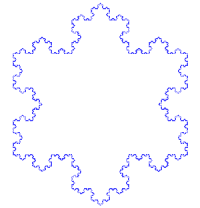
A görbét úgy állíthatjuk elő, hogy egy szabályos háromszög oldalait elharmadoljuk, majd a középső harmadára ismét egy szabályos háromszöget rajzolunk. Ezen háromszögek oldalait szintén harmadoljuk, és háromszöget rajzolunk rájuk. Ezt a végtelenségig folytatjuk. A görbe hossza az n-edik lépés után $(4/3)^{n}$. A határértékként kapott görbe végtelenül finoman strukturált, és csak közelítőleg lehet ábrázolni. Azok a pontok alkotják, amiket egy iterációs lépés után a további iterációs lépések megőriznek, vagy torlódási pontjai ennek a ponthalmaznak. Sokszor ennek az önmagába záródó görbének harmadát hívják Koch-görbének.

Tulajdonságai

Egyik tulajdonsága a skálafüggetlenség, a másik pedig különösen érdekes: végtelen lépés után a görbe hossza végtelen lesz, de sosem metszi önmagát, és véges térrészen marad: tehát véges területen végtelen hosszú lesz. Hausdorff-dimenziója ${\frac {\log(4)}{\log(3)}}\approx 1{,}26$. Szigorúan önhasonló, egyes részeit felnagyítva mindig ugyanaz a struktúra kerül elő. A Koch-görbe folytonos, mert a konstrukciójából adódóan van folytonos függvényeknek egy sorozata, amely egyenletesen tart hozzá. Ellenben sehol sem differenciálható, mert bármely kis szakaszán van egy töréspont, ahol a görbe 60 fokban megtörik.

A Koch-sziget területe

Az első hat iteráció látható

Jelölje s a kiindulási háromszög oldalának hosszát! Ekkor a kiindulási háromszög területe ${\frac {s^{2}{\sqrt {3}}}{4}}$ . Minden új iterációban az új kis háromszögek oldalhossza 1/3-a az előző iterációban kapott háromszögekének. Mivel a szabályos háromszögek területe négyzetesen függ az oldalhosszuktól, az új háromszögek területe egyenként 1/9-része az előző iterációban nyert háromszögek egyikének. A kis háromszögek száma minden iterációban megnégyszereződik. Mivel az első iterációban három háromszög keletkezik, az n-edik iterációban keletkező háromszögek száma $3\cdot 4^{n-1}$. Összetéve adódik az iterációs formula:

$A_{n}=A_{0}+{\frac {3\cdot 4^{n-1}}{9^{n}}}A_{0}\quad n\geq 1\,,$

ahol $A_{0}$ a kiindulási háromszög területe.

$A_{n}=A_{0}+\sum _{k=1}^{n}{\frac {3\cdot 4^{n-1}}{9^{n}}}A_{0}=\left(1+{\frac {3}{4}}\sum _{k=1}^{n}\left({\frac {4}{9}}\right)^{k}\right)A_{0}=\left(1+{\frac {1}{3}}\sum _{k=0}^{n-1}\left({\frac {4}{9}}\right)^{k}\right)A_{0}\,\,,$

$A_{n}=A_{0}\left(1+{\frac {3}{5}}\left(1-\left({\frac {4}{9}}\right)^{n}\right)\right)={\frac {A_{0}}{5}}\left(8-3\left({\frac {4}{9}}\right)^{n}\right)\,.$

Határértékben, ha n tart a végtelenbe, akkor 4/9 hatványainak összegeként 4/5 adódik. Ezzel

$\lim _{n\rightarrow \infty }A_{n}={\frac {A_{0}}{5}}\left(8-3\left({\frac {4}{9}}\right)^{n}\right)={\frac {8}{5}}A_{0}\,.$

Tehát a hópehelygörbe által körülzárt Koch-sziget területe a kiindulási háromszög területének 8/5 része, vagy az eredeti háromszög oldalhosszával kifejezve ${\frac {2s^{2}{\sqrt {3}}}{5}}$. Így a végtelenül hosszú hópehelygörbe egy véges területű síkdarabot ölel körül.

Geometriai sor határértékeként

Egy lépésben az új háromszögek száma egyenlő az előző lépésben kapott oldalak számával, ami lépésenként négyszeresére nő. Ezek területe az előző háromszög területének kilencedrésze. Jelölje T a kiindulási területet:

$T_{\infty }=T+3{\frac {T}{9}}+3\cdot 4{\frac {T}{9^{2}}}+3\cdot 4^{2}{\frac {T}{9^{3}}}+...=T+3\lim _{n\rightarrow \infty }\left({\frac {T}{9}}\sum _{k=0}^{n}\left({\frac {4}{9}}\right)^{k}\right)=T+{\frac {T}{3}}\cdot {\frac {1}{1-{\frac {4}{9}}}}={\frac {8T}{5}}$

Változatai

A Koch-görbéhez hasonlóan több más fraktál is készíthető:

Változat	Kép	Konstrukció
1D, 85°-os szög	Cesaro fractal	A Cesaro-fraktál a Koch-görbe variánsa, ahol az elfordulási szög 60° és 90° között változtatható (itt 85°).
1D, 90°-os szög	Quadratic type 1 curve	Kvadratikus Koch-görbe. Az első két iteráció
1D, 90°-os szög	Quadratic type 2 curve	Az első két iteráció. Hausdorff-dimenziója pontosan 1,5 és így éppen félúton van 1 és 2 között; ezért gyakran rajta tanulmányozzák a tört dimenziós fraktálok fizikai tulajdonságait.
2D, háromszögek	von Koch surface	A Koch-görbe természetes módon két dimenzióra kiterjesztett változata
2D, 90°-os szög	Quadratic type 1 surface	A kvadratikus görbe kiterjesztése. Az ábra a második iterációt mutatja.
2D, 90°-os szög	Quadratic type 2 surface	A kvadratikus görbe kiterjesztése. Az ábra az első iterációt mutatja.
2D, gömbök	Haines sphereflake (large green object)	Eric Haines térbeli, gömböket használó Koch-fraktálja

Források

• Helge von Koch: Une courbe continue sans tangente, obtenue par une construction géometrique élémentaire. Arkiv för Matematik 1 (1904) 681-704.
• Helge von Koch: Une méthode géométrique élémentaire pour l'étude de certaines questions de la théorie des courbes planes. Acta Mathematica 30 (1906) 145-174.
• Hópehelygörbe a MathWorldön

További információk

Koch-görbére hasonló fraktálok vizsgálata