Illeszkedési gráf
A matematika, azon belül a kombinatorika és gráfelmélet területén illeszkedési gráf, incidenciagráf vagy Levi-gráf (Levi graph vagy incidence graph) alatt egy illeszkedési struktúrához tartozó páros gráf értendő.[1][2] Egy illeszkedési geometria vagy projektív konfiguráció pontjaiból és egyeneseiből gráfot alkotunk oly módon, hogy a gráf minden csúcsa egy pontnak vagy egyenesnek felel meg, élei pedig a pontok és egyenesek közötti illeszkedéseknek. A Levi-gráf nevet F. W. Leviről kapták, aki 1942-ben írt róluk.[1][3]
| Illeszkedési gráf | |
 | |
| A Papposz-gráf, a Papposz-konfigurációból képezett 18 csúcsú illeszkedési gráf. Az egy betűvel jelölt csúcsok a konfiguráció egy pontjának, a három betűvel jelölt csúcsok a konfiguráció három ponton átmenő egyeneseinek felelnek meg. | |
| Derékbőség | ≥ 6 |
| Egyéb | 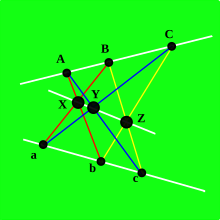 |
Pontok és egyenesek illeszkedési gráfjai általában legalább 6-os girthparaméterrel (bőséggel) rendelkeznek: bármely 4-kör ugyanazon a két ponton átmenő két egyenesnek felelne meg. Megfordítva, bármely, legalább 6 girthű páros gráf tekinthető egy absztrakt illeszkedési struktúra Levi-gráfjának.[1] A geometrikai konfigurációk Levi-gráfjai biregulárisak, és minden, legalább 6 bőségű bireguláris gráf tekinthető egy absztrakt konfiguráció Levi-gráfjának.[4]
Illeszkedési gráfok más incidenciastruktúrákhoz is definiálhatók, például az euklideszi tér síkjai és pontjai közötti illeszkedésekre. Minden illeszkedési gráfhoz tartozik egy ekvivalens hipergráf és vice versa.
Példák
szerkesztés- A Desargues-gráf a 10 pontból és 10 egyenesből álló Desargues-konfiguráció Levi-gráfja. MInden egyenesen 3 pont van és minden ponton 3 egyenes megy át. A 3-reguláris, 20 csúcsból álló Desargues-gráf tekinthető a G(10,3) általánosított Petersen-gráfnak vagy az 5,2 paraméterű páros Kneser-gráfnak is.
- A Heawood-gráf a Fano-sík Levi-gráfja. A (3,6)-cage-ként is ismert gráf 3-reguláris és 14 csúcsa van.
- A Möbius–Kantor-gráf az euklideszi síkban egyenes vonalakkal nem lerajzolható, 8 pontból és 8 egyenesből álló Möbius–Kantor-konfiguráció Levi-gráfja. 3-reguláris és 16 csúcsa van.
- A Papposz-gráf a 9 pontból és 9 egyenesből álló Papposz-konfiguráció Levi-gráfja. A Desargues-konfigurációhoz hasonlóan minden egyenesen 3 pont van és minden ponton 3 egyenes megy át. 3-reguláris és 18 csúcsa van.
- A Gray-gráf egy olyan konfiguráció Levi-gráfja, ami 27, R3-beli 3×3×3-as rácspontból és a köztük lévő 27 merőleges egyenesből áll. 3-reguláris és 54 csúcsa van.
- A Tutte–Coxeter-gráf a Cremona–Richmond-konfiguráció Levi-gráfja. A (3,8)-cage-ként is ismert gráf 3-regurláis és 30 csúcsa van.
- A Q4, azaz a négydimenziós hiperkockagráf a két, kölcsönösen egymásba írt tetraéder pontjai és síkjai által alkotott Möbius-konfiguráció Levi-gráfja.
- A 112 csúcsú Ljubljana-gráf a Ljubljana-konfiguráció Levi-gráfja. Az 56 egyenesből és 56 pontból álló konfigurációban minden egyenesen pontosan 3 pont van, minden ponton pontosan 3 egyenes megy át és bármely két egyenes legfeljebb egy pontban metszi egymást.[5]
Fordítás
szerkesztés- Ez a szócikk részben vagy egészben a Levi graph című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek
szerkesztés- ↑ a b c Grünbaum, Branko (2006), "Configurations of points and lines", The Coxeter Legacy, Providence, RI: American Mathematical Society, pp. 179–225. See in particular p. 181.
- ↑ Polster, Burkard (1998), A Geometrical Picture Book, Universitext, New York: Springer-Verlag, p. 5, ISBN 0-387-98437-2, doi:10.1007/978-1-4419-8526-2, <https://books.google.com/books?id=2PtPG4qjfZAC&pg=PA5>.
- ↑ Levi, F. W. (1942), Finite Geometrical Systems, Calcutta: University of Calcutta.
- ↑ Gropp, Harald (2007), "VI.7 Configurations", in Colbourn, Charles J. & Dinitz, Jeffrey H., Handbook of combinatorial designs (Second ed.), Discrete Mathematics and its Applications (Boca Raton), Chapman & Hall/CRC, Boca Raton, Florida, pp. 353–355.
- ↑ Conder, M.; Malnič, A. & Marušič, D. et al. (2002), The Ljubljana Graph, IMFM Preprint 40-845, University of Ljubljana Department of Mathematics, <http://www.imfm.si/preprinti/PDF/00845.pdf>.
További információk
szerkesztés- Weisstein, Eric W.: Levi Graph (angol nyelven). Wolfram MathWorld