Súlyfüggvény

A súlyfüggvény, más néven impulzusválasz, egy jelátviteli rendszernek az impulzusfüggvényre adott válasza, az átmeneti függvény deriváltja. Rendszerjellemző, hálózatfüggvény. Ha a nulla időpillanat előtt nem nulla értékű, akkor a rendszer nem kauzális. Laplace transzformáltja az átviteli függvény.

Bemeneti vizsgálójel: a Dirac delta

Arányos (proporcionális) viselkedésű tag válaszfüggvénye $\delta _{a}(x)={\frac {1}{a{\sqrt {\pi }}}}\mathrm {e} ^{-x^{2}/a^{2}}$ ahol a tart a nullához: $a\to 0$

A matematikai leírásmód elfogadja, hogy a függvénynek a nulla időpont előtt is lehet értéke. Ezt mínusz nulla időpontnak nevezzük. Mínusz nulla a függvény határértéke, amikor az idő a negatív tartományból közelít a nullához, és azt minden határon túl megközelíti. Tekintettel arra, hogy a függvény az idő vonatkozásában szimmetrikus, értéke a plusz nulla időpontban azonos. Ugyanakkor egyetlen reális eszközről sem tételezhetjük fel, hogy „tudja”, mekkora a válaszfüggvény, mielőtt az az esemény bekövetkezett volna, amelyre választ ad. Ez a kauzalitás (az ok–okozati összefüggés) megsértésének esete volna. A szabályozáselmélet annyiban egyszerűsíti a problémát, hogy a függvénynek csupán a nullánál nagyobb időpontra vonatkozó értékeit vizsgálja.

Szabályozott szakasz viselkedése

A súlyfüggvény lehetőséget ad a szabályozott szakasz bármely tagja dinamikus viselkedésének leírására. Tipikus felhasználása: impulzusjel bevitele alapjelként. A rendszer válaszfüggvénye:

• arányos tag esetén a bemeneti és a kimeneti jel között csak az átviteli tényező (az erősítés) értéke teremt kapcsolatot
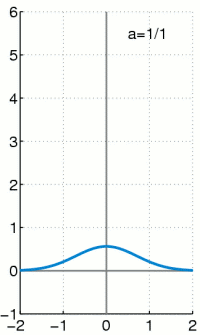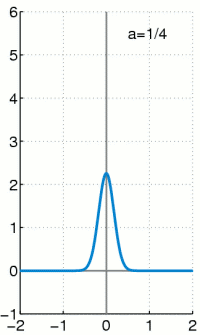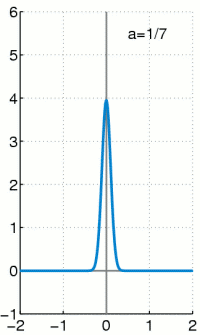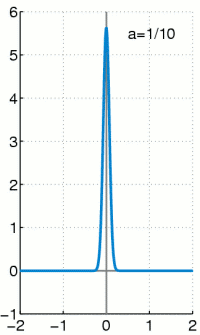
  • tehetetlenséggel rendelkező arányos tag esetén az impulzusfüggvény szélessége (időbeli kiterjedése) a nullánál nagyobb (lásd a mellékelt ábrán a Gauss közelítést)
• integráló tagnál a kimenő jel formája hasonló az egységugrás jelhez
• differenciáló tagra nincs értelme megvizsgálni (a kimenet időfüggvénye egy kettős impulzusfüggvény volna), nincs reális megvalósítása

Források

http://www.kislexikon.hu/sulyfuggveny.html

Kapcsolódó szócikkek

• Átviteli függvény
• Átviteli karakterisztika
• Bode-diagram