A trigonometrikus azonosságok szögfüggvények között fennálló matematikai összefüggések (egyenlőségek, azonosságok). Ezek az azonosságok hasznosak szögfüggvényeket tartalmazó kifejezések egyszerűbb alakra hozásakor. Egyéb függvények integrálásakor is alkalmazzák őket, amikor bizonyos kifejezéseket trigonometrikus kifejezésekkel helyettesítünk, majd a kapott integrált trigonometrikus azonosságokkal egyszerűsítjük.
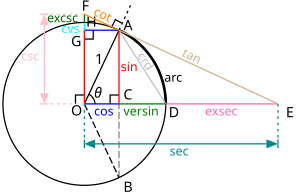
Egy szög (θ) minden trigonometriai függvénye megszerkeszthető az origó középpontú egységkör segítségével.
Az alábbi jelöléseket használjuk a hat szögfüggvényre:
szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg), szekáns (sec) és koszekáns (csc). Egyszerűség kedvéért csak a szinusz esetét mutatja az alábbi táblázat.
Jelölések
Olvasd
Leírás
Definíció
sin²(x)
„szinusz négyzet x”
a szinusz négyzete; szinusz a második hatványon
sin²(x ) = (sin(x))²
arcsin(x)
„arkuszszinusz x ”
a szinusz inverz függvénye
arcsin(x) = y akkor és csak akkor, ha sin(y) = x és
−
π
2
≤
y
≤
π
2
{\displaystyle -{\pi \over 2}\leq y\leq {\pi \over 2}}
(sin(x ))‒1
„szinusz x a (-1)-edik hatványon”
a szinusz reciproka ;
(sin(x ))‒1 = 1 / sin(x ) = csc(x )
arcsin(x ) így is írható: sin−1 (x ); ezt nem szabad összetéveszteni a (sin(x ))‒1 -nel.
t
g
(
x
)
=
sin
(
x
)
cos
(
x
)
c
t
g
(
x
)
=
cos
(
x
)
sin
(
x
)
=
1
t
g
(
x
)
sec
(
x
)
=
1
cos
(
x
)
csc
(
x
)
=
1
sin
(
x
)
{\displaystyle {\begin{aligned}\mathrm {tg} (x)&={\frac {\sin(x)}{\cos(x)}}&\quad \mathrm {ctg} (x)&={\frac {\cos(x)}{\sin(x)}}={\frac {1}{\mathrm {tg} (x)}}\\\sec(x)&={\frac {1}{\cos(x)}}&\quad \csc(x)&={\frac {1}{\sin(x)}}\end{aligned}}}
További részletekről lásd trigonometrikus függvények .
Az egységsugarú körből egyszerű belátni:
A szinusz, koszinusz, szekáns, és koszekáns függvények 2π (egy teljes kör) szerint periodikusak: ha
k
{\displaystyle k}
egész szám akkor
sin
(
x
)
=
sin
(
x
+
2
k
π
)
cos
(
x
)
=
cos
(
x
+
2
k
π
)
sec
(
x
)
=
sec
(
x
+
2
k
π
)
csc
(
x
)
=
csc
(
x
+
2
k
π
)
{\displaystyle {\begin{aligned}\sin(x)&=\sin(x+2k\pi )\\\cos(x)&=\cos(x+2k\pi )\\\sec(x)&=\sec(x+2k\pi )\\\csc(x)&=\csc(x+2k\pi )\\\end{aligned}}}
A tangens- és kotangensfüggvények π szerint periodikusak: ha
k
{\displaystyle k}
t
g
(
x
)
=
t
g
(
x
+
k
π
)
c
t
g
(
x
)
=
c
t
g
(
x
+
k
π
)
{\displaystyle {\begin{aligned}\mathrm {tg} (x)&=\mathrm {tg} (x+k\pi )\\\mathrm {ctg} (x)&=\mathrm {ctg} (x+k\pi )\\\end{aligned}}}
sin
(
−
x
)
=
−
sin
(
x
)
sin
(
π
2
−
x
)
=
cos
(
x
)
sin
(
π
−
x
)
=
+
sin
(
x
)
cos
(
−
x
)
=
+
cos
(
x
)
cos
(
π
2
−
x
)
=
sin
(
x
)
cos
(
π
−
x
)
=
−
cos
(
x
)
t
g
(
−
x
)
=
−
t
g
(
x
)
t
g
(
π
2
−
x
)
=
c
t
g
(
x
)
t
g
(
π
−
x
)
=
−
t
g
(
x
)
c
t
g
(
−
x
)
=
−
c
t
g
(
x
)
c
t
g
(
π
2
−
x
)
=
t
g
(
x
)
c
t
g
(
π
−
x
)
=
−
c
t
g
(
x
)
sec
(
−
x
)
=
+
sec
(
x
)
sec
(
π
2
−
x
)
=
csc
(
x
)
sec
(
π
−
x
)
=
−
sec
(
x
)
csc
(
−
x
)
=
−
csc
(
x
)
csc
(
π
2
−
x
)
=
sec
(
x
)
csc
(
π
−
x
)
=
+
csc
(
x
)
{\displaystyle {\begin{aligned}\sin(-x)&=-\sin(x)&\sin \left({\tfrac {\pi }{2}}-x\right)&=\cos(x)&\sin \left(\pi -x\right)&=+\sin(x)\\\cos(-x)&=+\cos(x)&\cos \left({\tfrac {\pi }{2}}-x\right)&=\sin(x)&\cos \left(\pi -x\right)&=-\cos(x)\\\mathrm {tg} (-x)&=-\mathrm {tg} (x)&\mathrm {tg} \left({\tfrac {\pi }{2}}-x\right)&=\mathrm {ctg} (x)&\mathrm {tg} \left(\pi -x\right)&=-\mathrm {tg} (x)\\\mathrm {ctg} (-x)&=-\mathrm {ctg} (x)&\mathrm {ctg} \left({\tfrac {\pi }{2}}-x\right)&=\mathrm {tg} (x)&\mathrm {ctg} \left(\pi -x\right)&=-\mathrm {ctg} (x)\\\sec(-x)&=+\sec(x)&\sec \left({\tfrac {\pi }{2}}-x\right)&=\csc(x)&\sec \left(\pi -x\right)&=-\sec(x)\\\csc(-x)&=-\csc(x)&\csc \left({\tfrac {\pi }{2}}-x\right)&=\sec(x)&\csc \left(\pi -x\right)&=+\csc(x)\end{aligned}}}
Eltolás π/2 és π szöggel:
sin
(
x
+
π
2
)
=
+
cos
(
x
)
sin
(
x
+
π
)
=
−
sin
(
x
)
cos
(
x
+
π
2
)
=
−
sin
(
x
)
cos
(
x
+
π
)
=
−
cos
(
x
)
t
g
(
x
+
π
2
)
=
−
c
t
g
(
x
)
t
g
(
x
+
π
)
=
+
t
g
(
x
)
c
t
g
(
x
+
π
2
)
=
−
t
g
(
x
)
c
t
g
(
x
+
π
)
=
+
c
t
g
(
x
)
sec
(
x
+
π
2
)
=
−
csc
(
x
)
sec
(
x
+
π
)
=
−
sec
(
x
)
csc
(
x
+
π
2
)
=
+
sec
(
x
)
csc
(
x
+
π
)
=
−
csc
(
x
)
{\displaystyle {\begin{aligned}\sin \left(x+{\tfrac {\pi }{2}}\right)&=+\cos(x)&\sin \left(x+\pi \right)&=-\sin(x)\\\cos \left(x+{\tfrac {\pi }{2}}\right)&=-\sin(x)&\cos \left(x+\pi \right)&=-\cos(x)\\\mathrm {tg} \left(x+{\tfrac {\pi }{2}}\right)&=-\mathrm {ctg} (x)&\mathrm {tg} \left(x+\pi \right)&=+\mathrm {tg} (x)\\\mathrm {ctg} \left(x+{\tfrac {\pi }{2}}\right)&=-\mathrm {tg} (x)&\mathrm {ctg} \left(x+\pi \right)&=+\mathrm {ctg} (x)\\\sec \left(x+{\tfrac {\pi }{2}}\right)&=-\csc(x)&\sec \left(x+\pi \right)&=-\sec(x)\\\csc \left(x+{\tfrac {\pi }{2}}\right)&=+\sec(x)&\csc \left(x+\pi \right)&=-\csc(x)\end{aligned}}}
Néhány esetben fontos tudni, hogy ugyanolyan periódusú, de különböző fázisban lévő szinusz hullámok lineáris kombinációja szintén ugyanolyan periódusú, de más fázisszögű szinusz hullámot ad. Szinusz és koszinusz hullámok lineáris kombinációjakor ez írható:
a
sin
x
+
b
cos
x
=
a
2
+
b
2
⋅
sin
(
x
+
φ
)
,
{\displaystyle a\sin x+b\cos x={\sqrt {a^{2}+b^{2}}}\cdot \sin(x+\varphi )\ ,}
ahol
φ
=
{
a
r
c
t
g
(
b
/
a
)
,
ha
a
≥
0
;
a
r
c
t
g
(
b
/
a
)
±
π
,
ha
a
<
0.
{\displaystyle \varphi =\left\{{\begin{matrix}{\rm {arctg}}(b/a),&&{\mbox{ha }}a\geq 0;\;\\\mathrm {arctg} (b/a)\pm \pi ,&&{\mbox{ha }}a<0.\;\end{matrix}}\right.\;}
Általánosabban tetszőleges fázisszögre írható:
a
sin
x
+
b
sin
(
x
+
α
)
=
c
sin
(
x
+
β
)
,
{\displaystyle a\sin x+b\sin(x+\alpha )=c\sin(x+\beta )\ ,}
ahol
c
=
a
2
+
b
2
+
2
a
b
cos
α
,
{\displaystyle c={\sqrt {a^{2}+b^{2}+2ab\cos \alpha }},}
és
β
=
a
r
c
t
g
(
b
sin
α
a
+
b
cos
α
)
.
{\displaystyle \beta ={\rm {arctg}}\left({\frac {b\sin \alpha }{a+b\cos \alpha }}\right).}
Ezek az azonosságok a Pitagorasz-tételen alapulnak.
sin
2
(
x
)
+
cos
2
(
x
)
=
1
t
g
2
(
x
)
+
1
=
sec
2
(
x
)
c
t
g
2
(
x
)
+
1
=
csc
2
(
x
)
{\displaystyle {\begin{aligned}&\sin ^{2}(x)+\cos ^{2}(x)=1\\&\mathrm {tg} ^{2}(x)+1=\sec ^{2}(x)\\&\mathrm {ctg} ^{2}(x)+1=\csc ^{2}(x)\end{aligned}}}
A második egyenlőség az elsőből úgy kapható, ha mindkét oldalt osztjuk cos2 (x )-szel. A harmadik egyenlőséghez az elsőt sin2 (x )-szel kell osztani.
szerkesztés
Két (vagy több) szög (ill. argumentum) összegének és különbségének trigonometrikus függvényei kifejezhetőek az argumentumok szögfüggvényeinek bizonyos (általában racionális egész-, vagy, a tangens és kotangens esetében, racionális tört-) kifejezéseiként, ezek az addíciós azonosságok. Lehet őket már elemi geometriai úton is igazolni, de a teljesen szigorú igazolás ez esetben kissé nehézkes, mert több eset szétválasztását igényli (ettől eltekintve azonban egyszerű, mert csak a hasonlóság definíciójának és esetleg a polinomiális tétel speciális eseteinek ismeretére - azaz elég alapfokú geometriai és algebrai jártasságra - van szükség). Igazolni lehet az addíciós képleteiket a differenciálegyenletes definíciókra hagyatkozva, vagy az Euler-formulával is, bár ezek igazolása mélyebb matematikai ismereteket igényel.
sin
(
x
±
y
)
=
sin
(
x
)
cos
(
y
)
±
cos
(
x
)
sin
(
y
)
{\displaystyle \sin(x\pm y)=\sin(x)\cos(y)\pm \cos(x)\sin(y)\,}
(Ha "+" szerepel a bal oldalon, akkor "+" van a jobb oldalon is,és fordítva.)
cos
(
x
±
y
)
=
cos
(
x
)
cos
(
y
)
∓
sin
(
x
)
sin
(
y
)
{\displaystyle \cos(x\pm y)=\cos(x)\cos(y)\mp \sin(x)\sin(y)\,}
(Ha "+" szerepel a bal oldalon, akkor "-" van a jobb oldalon, és fordítva.)
t
g
(
x
±
y
)
=
t
g
(
x
)
±
t
g
(
y
)
1
∓
t
g
(
x
)
t
g
(
y
)
{\displaystyle \mathrm {tg} (x\pm y)={\frac {\mathrm {tg} (x)\pm \mathrm {tg} (y)}{1\mp \mathrm {tg} (x)\mathrm {tg} (y)}}}
A bizonyítások lehetségesek a skaláris szorzat, annak tulajdonságai, és egyszerűbb trigonometrikus összefüggések felhasználásával is:
Vegyünk fel egy Descartes-féle derékszögű koordináta-rendszert az euklideszi síkon és két egység hosszú vektort, melyekhez tartozó origó középpontú helyvektoroknak az x-tengely pozitív felével bezárt forgásszögeinek ívmértékei x és y.
Írjuk fel ennek a két vektornak a skaláris szorzatát egyrészt a definíció alapján (a vektorok abszolút értékeinek és a bezárt szögük koszinuszának a szorzata), másrészt a koordinátáikkal (az első és a második koordináták szorzatainak az összege)
Ügyeljünk arra, hogy több eset lehetséges x, y és a 0 egymáshoz viszonyított értékeinek függvényében.
Ebből kapjuk a két szám különbségének koszinuszára vonatkozó azonosságot. Ezután ebből x+y = x-(-y), a pótszögek ívmértékeinek szögfüggvényei közötti összefüggések, illetve a tangens és kotangens szögfüggvények definícióinak felhasználásával kapjuk a többi azonosságot.
Részletes bizonyítást olvashatunk (bár csak az x>y>0 esetre vonatkozóan) a Hajnal-Számadó-Békéssy: Matematika a gimnáziumok 11. évfolyama számára című tankönyv 90-91. oldalain (Nemzeti Tankönyvkiadó, Budapest, 2005).
Az alábbiakat le lehet vezetni úgy, hogy az összegképletben x = y helyettesítést végzünk és felhasználjuk a Pitagorasz-tételt. Vagy felírjuk a de Moivre-formulát n = 2 esetre:
sin
(
2
x
)
=
2
sin
(
x
)
cos
(
x
)
{\displaystyle \sin(2x)=2\sin(x)\cos(x)\,}
cos
(
2
x
)
=
cos
2
(
x
)
−
sin
2
(
x
)
=
2
cos
2
(
x
)
−
1
=
1
−
2
sin
2
(
x
)
=
1
−
t
g
2
(
x
)
1
+
t
g
2
(
x
)
{\displaystyle \cos(2x)=\cos ^{2}(x)-\sin ^{2}(x)=2\cos ^{2}(x)-1=1-2\sin ^{2}(x)={\frac {1-\mathrm {tg} ^{2}(x)}{1+\mathrm {tg} ^{2}(x)}}\,}
t
g
(
2
x
)
=
2
t
g
(
x
)
1
−
t
g
2
(
x
)
{\displaystyle \mathrm {tg} (2x)={\frac {2\mathrm {tg} (x)}{1-\mathrm {tg} ^{2}(x)}}\,}
c
t
g
(
2
x
)
=
c
t
g
(
x
)
−
t
g
(
x
)
2
{\displaystyle \mathrm {ctg} (2x)={\frac {\mathrm {ctg} (x)-\mathrm {tg} (x)}{2}}\,}
A kétszeres szög-képletek segítségével pitagoraszi számhármasokat is találhatunk.
Ha (a , b , c ) egy derékszögű háromszög oldalai, akkor (a 2 ‒ b 2 , 2ab , c 2 ) szintén derékszögű háromszöget alkot, ahol B az a szög, melyet megdupláztunk.
Ha a 2 ‒ b 2 negatív, vegyük ellenkező előjellel és 2B helyett használjuk a 2B -t
Π
{\displaystyle \Pi }
sin
(
3
x
)
=
3
sin
(
x
)
−
4
sin
3
(
x
)
{\displaystyle \sin(3x)=3\sin(x)-4\sin ^{3}(x)\,}
cos
(
3
x
)
=
4
cos
3
(
x
)
−
3
cos
(
x
)
{\displaystyle \cos(3x)=4\cos ^{3}(x)-3\cos(x)\,}
t
g
(
3
x
)
=
3
t
g
(
x
)
−
t
g
3
(
x
)
1
−
3
t
g
2
(
x
)
{\displaystyle \mathrm {tg} (3x)={\frac {3\mathrm {tg} (x)-\mathrm {tg} ^{3}(x)}{1-3\mathrm {tg} ^{2}(x)}}}
sin
n
θ
=
∑
k
=
0
n
(
n
k
)
cos
k
θ
sin
n
−
k
θ
sin
(
1
2
(
n
−
k
)
π
)
{\displaystyle \sin n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\sin \left({\frac {1}{2}}(n-k)\pi \right)}
cos
n
θ
=
∑
k
=
0
n
(
n
k
)
cos
k
θ
sin
n
−
k
θ
cos
(
1
2
(
n
−
k
)
π
)
{\displaystyle \cos n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\cos \left({\frac {1}{2}}(n-k)\pi \right)}
A többszörös szög tangense és kotangense a következő rekurzióval vezethető vissza az egyszeres szög tangensére:
t
g
(
n
+
1
)
θ
=
t
g
n
θ
+
t
g
θ
1
−
t
g
n
θ
t
g
θ
.
{\displaystyle \mathrm {tg} \,(n{+}1)\theta ={\frac {\mathrm {tg} n\theta +\mathrm {tg} \theta }{1-\mathrm {tg} n\theta \,\mathrm {tg} \theta }}.}
c
t
g
(
n
+
1
)
θ
=
c
t
g
n
θ
c
t
g
θ
−
1
c
t
g
n
θ
+
c
t
g
θ
.
{\displaystyle \mathrm {ctg} \,(n{+}1)\theta ={\frac {\mathrm {ctg} n\theta \,\mathrm {ctg} \theta -1}{\mathrm {ctg} n\theta +\mathrm {ctg} \theta }}.}
Ha Tn az n ik Csebisev-polinom , akkor
cos
(
n
x
)
=
T
n
(
cos
(
x
)
)
.
{\displaystyle \cos(nx)=T_{n}(\cos(x)).\,}
Ha S n n -ik kiterjesztett polinom ,(wd)
sin
2
(
n
θ
)
=
S
n
(
sin
2
θ
)
.
{\displaystyle \sin ^{2}(n\theta )=S_{n}(\sin ^{2}\theta ).\,}
A de Moivre-formula :
cos
(
n
x
)
+
i
sin
(
n
x
)
=
(
cos
(
x
)
+
i
sin
(
x
)
)
n
{\displaystyle \cos(nx)+i\sin(nx)=(\cos(x)+i\sin(x))^{n}\,}
Ha az előző képletekbe x helyére x /2-t helyettesítünk, akkor cos(x /2)-re és sin(x /2)-re megoldva a következőt kapjuk:
cos
(
x
2
)
=
±
1
+
cos
(
x
)
2
{\displaystyle \cos \left({\frac {x}{2}}\right)=\pm \,{\sqrt {\frac {1+\cos(x)}{2}}}}
sin
(
x
2
)
=
±
1
−
cos
(
x
)
2
{\displaystyle \sin \left({\frac {x}{2}}\right)=\pm \,{\sqrt {\frac {1-\cos(x)}{2}}}}
Ezek a fél-szög képletek. Továbbá
t
g
(
x
2
)
=
sin
(
x
/
2
)
cos
(
x
/
2
)
=
±
1
−
cos
x
1
+
cos
x
.
(
1
)
{\displaystyle \mathrm {tg} \left({\frac {x}{2}}\right)={\sin(x/2) \over \cos(x/2)}=\pm \,{\sqrt {1-\cos x \over 1+\cos x}}.\qquad \qquad (1)}
Szorozzuk be a számlálót és a nevezőt a gyökjel alatt 1 + cos x -szel, majd hozzuk egyszerűbb alakra a Pitagorasz-tétellel:
t
g
(
x
2
)
=
±
(
1
−
cos
x
)
(
1
+
cos
x
)
(
1
+
cos
x
)
(
1
+
cos
x
)
=
±
1
−
cos
2
x
(
1
+
cos
x
)
2
{\displaystyle \mathrm {tg} \left({\frac {x}{2}}\right)=\pm \,{\sqrt {(1-\cos x)(1+\cos x) \over (1+\cos x)(1+\cos x)}}=\pm \,{\sqrt {1-\cos ^{2}x \over (1+\cos x)^{2}}}}
=
sin
x
1
+
cos
x
.
{\displaystyle ={\sin x \over 1+\cos x}.}
Hasonlóképpen az (1) egyenlőség számlálóját és nevezőjét a gyökjel alatt szorozzuk be 1 ‒ cos x -szel, egyszerűsítés után írható:
t
g
(
x
2
)
=
±
(
1
−
cos
x
)
(
1
−
cos
x
)
(
1
+
cos
x
)
(
1
−
cos
x
)
=
±
(
1
−
cos
x
)
2
(
1
−
cos
2
x
)
{\displaystyle \mathrm {tg} \left({\frac {x}{2}}\right)=\pm \,{\sqrt {(1-\cos x)(1-\cos x) \over (1+\cos x)(1-\cos x)}}=\pm \,{\sqrt {(1-\cos x)^{2} \over (1-\cos ^{2}x)}}}
=
1
−
cos
x
sin
x
.
{\displaystyle ={1-\cos x \over \sin x}.}
Így a tangens fél-szög képletek a következők:
t
g
(
x
2
)
=
sin
(
x
)
1
+
cos
(
x
)
=
1
−
cos
(
x
)
sin
(
x
)
.
{\displaystyle \mathrm {tg} \left({\frac {x}{2}}\right)={\frac {\sin(x)}{1+\cos(x)}}={\frac {1-\cos(x)}{\sin(x)}}.}
Hasonlóan írható:
t
g
(
x
2
)
=
csc
(
x
)
−
c
t
g
(
x
)
,
{\displaystyle \mathrm {tg} \left({x \over 2}\right)=\csc(x)-\mathrm {ctg} (x),}
c
t
g
(
x
2
)
=
csc
(
x
)
+
c
t
g
(
x
)
.
{\displaystyle \mathrm {ctg} \left({x \over 2}\right)=\csc(x)+\mathrm {ctg} (x).}
Ha bevezetjük az alábbi jelölést:
t
=
t
g
(
x
2
)
,
{\displaystyle t=\mathrm {tg} \left({\frac {x}{2}}\right),}
akkor
sin
(
x
)
=
2
t
1
+
t
2
{\displaystyle \sin(x)={\frac {2t}{1+t^{2}}}}
és
cos
(
x
)
=
1
−
t
2
1
+
t
2
{\displaystyle \cos(x)={\frac {1-t^{2}}{1+t^{2}}}}
és
t
g
(
x
)
=
2
t
1
−
t
2
{\displaystyle \mathrm {tg} (x)={\frac {2t}{1-t^{2}}}}
és
e
i
x
=
1
+
i
t
1
−
i
t
.
{\displaystyle e^{ix}={\frac {1+it}{1-it}}.}
szerkesztés
Helyettesítsünk x helyére (x + y ) / 2-t és y helyére (x – y ) / 2-t a szorzat-összeg képletbe:
cos
(
x
)
+
cos
(
y
)
=
2
cos
(
x
+
y
2
)
cos
(
x
−
y
2
)
{\displaystyle \cos(x)+\cos(y)=2\cos \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)\;}
sin
(
x
)
+
sin
(
y
)
=
2
sin
(
x
+
y
2
)
cos
(
x
−
y
2
)
{\displaystyle \sin(x)+\sin(y)=2\sin \left({\frac {x+y}{2}}\right)\cos \left({\frac {x-y}{2}}\right)\;}
cos
(
x
)
−
cos
(
y
)
=
−
2
sin
(
x
+
y
2
)
sin
(
x
−
y
2
)
{\displaystyle \cos(x)-\cos(y)=-2\sin \left({x+y \over 2}\right)\sin \left({x-y \over 2}\right)\;}
sin
(
x
)
−
sin
(
y
)
=
2
cos
(
x
+
y
2
)
sin
(
x
−
y
2
)
{\displaystyle \sin(x)-\sin(y)=2\cos \left({x+y \over 2}\right)\sin \left({x-y \over 2}\right)\;}
t
g
(
x
)
+
t
g
(
y
)
=
sin
(
x
+
y
)
cos
(
x
)
⋅
cos
(
y
)
{\displaystyle \mathrm {tg} (x)+\mathrm {tg} (y)={\frac {\sin(x+y)}{\cos(x)\cdot \cos(y)}}}
Ha x , y és z egy tetszőleges háromszög szögei, vagy más szóval
ha
x
+
y
+
z
=
π
{\displaystyle {\mbox{ha }}x+y+z=\pi \,}
akkor
t
g
(
x
)
+
t
g
(
y
)
+
t
g
(
z
)
=
t
g
(
x
)
t
g
(
y
)
t
g
(
z
)
.
{\displaystyle {\mbox{akkor }}\mathrm {tg} (x)+\mathrm {tg} (y)+\mathrm {tg} (z)=\mathrm {tg} (x)\mathrm {tg} (y)\mathrm {tg} (z).\,}
Ha az x , y , z szögek valamelyike derékszög, akkor mindkét oldalt végtelennek kell tekinteni. Ez nem +∞ vagy -∞; itt több értelme van egy végtelen pontot hozzávenni a valós számegyeneshez, amit a tangensfüggvény akár a pozitív értékeken át nőve, akár a negatív értékeken át csökkenve elérhet. Ez a valós egyenes egypontos kompaktifikációja.
Ha
x
+
y
+
z
=
π
{\displaystyle {\mbox{Ha }}x+y+z=\pi \,}
akkor
sin
(
2
x
)
+
sin
(
2
y
)
+
sin
(
2
z
)
=
4
sin
(
x
)
sin
(
y
)
sin
(
z
)
.
{\displaystyle {\mbox{akkor }}\sin(2x)+\sin(2y)+\sin(2z)=4\sin(x)\sin(y)\sin(z).\,}
Szinusz és koszinusz számtani sorozat szerinti argumentummal:
sin
φ
+
sin
(
φ
+
α
)
+
sin
(
φ
+
2
α
)
+
⋯
+
sin
(
φ
+
n
α
)
=
sin
(
(
n
+
1
)
α
2
)
⋅
sin
(
φ
+
n
α
2
)
sin
α
2
.
{\displaystyle \sin {\varphi }+\sin {(\varphi +\alpha )}+\sin {(\varphi +2\alpha )}+\cdots +\sin {(\varphi +n\alpha )}={\frac {\sin {\left({\frac {(n+1)\alpha }{2}}\right)}\cdot \sin {(\varphi +{\frac {n\alpha }{2}})}}{\sin {\frac {\alpha }{2}}}}.}
cos
φ
+
cos
(
φ
+
α
)
+
cos
(
φ
+
2
α
)
+
⋯
+
cos
(
φ
+
n
α
)
=
sin
(
(
n
+
1
)
α
2
)
⋅
cos
(
φ
+
n
α
2
)
sin
α
2
.
{\displaystyle \cos {\varphi }+\cos {(\varphi +\alpha )}+\cos {(\varphi +2\alpha )}+\cdots +\cos {(\varphi +n\alpha )}={\frac {\sin {\left({\frac {(n+1)\alpha }{2}}\right)}\cdot \cos {(\varphi +{\frac {n\alpha }{2}})}}{\sin {\frac {\alpha }{2}}}}.}
Bármely a és b esetén:
a
cos
(
x
)
+
b
sin
(
x
)
=
a
2
+
b
2
cos
(
x
−
a
r
c
t
g
(
b
/
a
)
)
{\displaystyle a\cos(x)+b\sin(x)={\sqrt {a^{2}+b^{2}}}\cos(x-\mathrm {arc\,tg} (b/a))\;}
ahol arc tg(y , x ) az arc tg(y /x ) általánosítása, mely lefedi a teljes kört.
t
g
(
x
)
+
sec
(
x
)
=
t
g
(
x
2
+
π
4
)
.
{\displaystyle \mathrm {tg} (x)+\sec(x)=\mathrm {tg} \left({x \over 2}+{\pi \over 4}\right).}
A fenti azonosságot jó tudni, ha a Guderman-függvényre gondolunk.
Ha
x
+
y
+
z
=
π
{\displaystyle x+y+z=\pi }
c
t
g
(
x
)
c
t
g
(
y
)
+
c
t
g
(
y
)
c
t
g
(
z
)
+
c
t
g
(
z
)
c
t
g
(
x
)
=
1.
{\displaystyle \mathrm {ctg} (x)\mathrm {ctg} (y)+\mathrm {ctg} (y)\mathrm {ctg} (z)+\mathrm {ctg} (z)\mathrm {ctg} (x)=1.\,}
a
r
c
s
i
n
(
x
)
+
a
r
c
c
o
s
(
x
)
=
π
/
2
{\displaystyle \mathrm {arc\,sin} (x)+\mathrm {arc\,cos} (x)=\pi /2\;}
a
r
c
t
g
(
x
)
+
a
r
c
c
t
g
(
x
)
=
π
/
2
{\displaystyle \mathrm {arc\,tg} (x)+\mathrm {arc\,ctg} (x)=\pi /2\;}
a
r
c
t
g
(
x
)
+
a
r
c
t
g
(
1
/
x
)
=
{
π
/
2
,
ha
x
>
0
−
π
/
2
,
ha
x
<
0
{\displaystyle \mathrm {arc\,tg} (x)+\mathrm {arc\,tg} (1/x)=\left\{{\begin{matrix}\pi /2,&{\mbox{ha }}x>0\\-\pi /2,&{\mbox{ha }}x<0\end{matrix}}\right.}
a
r
c
t
g
(
x
)
+
a
r
c
t
g
(
y
)
=
a
r
c
t
g
(
x
+
y
1
−
x
y
)
+
{
π
,
ha
x
,
y
>
0
−
π
,
ha
x
,
y
<
0
0
,
egyebekben
{\displaystyle \mathrm {arc\,tg} (x)+\mathrm {arc\,tg} (y)=\mathrm {arc\,tg} \left({\frac {x+y}{1-xy}}\right)+\left\{{\begin{matrix}\pi ,&{\mbox{ha }}x,y>0\\-\pi ,&{\mbox{ha }}x,y<0\\0,&{\mbox{egyebekben }}\end{matrix}}\right.}
sin
[
a
r
c
c
o
s
(
x
)
]
=
1
−
x
2
{\displaystyle \sin[\mathrm {arc\,cos} (x)]={\sqrt {1-x^{2}}}\,}
cos
[
a
r
c
s
i
n
(
x
)
]
=
1
−
x
2
{\displaystyle \cos[\mathrm {arc\,sin} (x)]={\sqrt {1-x^{2}}}\,}
sin
[
a
r
c
t
g
(
x
)
]
=
x
1
+
x
2
{\displaystyle \sin[\mathrm {arc\,tg} (x)]={\frac {x}{\sqrt {1+x^{2}}}}}
cos
[
a
r
c
t
g
(
x
)
]
=
1
1
+
x
2
{\displaystyle \cos[\mathrm {arc\,tg} (x)]={\frac {1}{\sqrt {1+x^{2}}}}}
t
g
[
a
r
c
s
i
n
(
x
)
]
=
x
1
−
x
2
{\displaystyle \mathrm {tg} [\mathrm {arc\,sin} (x)]={\frac {x}{\sqrt {1-x^{2}}}}}
t
g
[
a
r
c
c
o
s
(
x
)
]
=
1
−
x
2
x
{\displaystyle \mathrm {tg} [\mathrm {arc\,cos} (x)]={\frac {\sqrt {1-x^{2}}}{x}}}
Minden szöggfüggvény kifejezhető közvetlenül bármely más szögfüggvénnyel. Ezek az összefüggések az inverz szögfüggvényekkel fejezhetők ki: legyen φ és ψ két szögfüggvény és legyen arcψ a ψ szögfüggvény inverze, ekkor írható: ψ(arcψ(x )) = x . Ezután a φ(arcψ(x )) kifejezhető x algebrai képletével. Ilyen képletek láthatók az alábbi táblázatban: φ a sorok első eleme lehet, ψ pedig az oszlopok első eleme.
Figyelem: A táblázatban minden oszlop (és nem sor ) bemenő értéke egy szög hat szögfüggvénye.
A tg , a ctg , a sec és a csc függvények értékei csak akkor számíthatók a táblázat alapján, ha az adott szögre értelmesek.
Konverziós képletek táblázata
φ
(
arc
ψ
(
x
)
)
{\displaystyle \varphi (\operatorname {arc} \,\psi (x))}
φ \ ψ
sin
cos
tg
csc
sec
ctg
sin
x
{\displaystyle x\ }
1
−
x
2
{\displaystyle {\sqrt {1-x^{2}}}}
x
1
+
x
2
{\displaystyle {x \over {\sqrt {1+x^{2}}}}}
1
x
{\displaystyle {1 \over x}}
1
−
x
2
x
{\displaystyle {{\sqrt {1-x^{2}}} \over x}}
1
1
+
x
2
{\displaystyle {1 \over {\sqrt {1+x^{2}}}}}
cos
1
−
x
2
{\displaystyle {\sqrt {1-x^{2}}}}
x
{\displaystyle x\ }
1
1
+
x
2
{\displaystyle {1 \over {\sqrt {1+x^{2}}}}}
x
2
−
1
x
{\displaystyle {{\sqrt {x^{2}-1}} \over x}}
1
x
{\displaystyle {1 \over x}}
x
1
+
x
2
{\displaystyle {x \over {\sqrt {1+x^{2}}}}}
tg
x
1
−
x
2
{\displaystyle {x \over {\sqrt {1-x^{2}}}}}
1
−
x
2
x
{\displaystyle {{\sqrt {1-x^{2}}} \over x}}
x
{\displaystyle x\ }
1
x
2
−
1
{\displaystyle {1 \over {\sqrt {x^{2}-1}}}}
x
2
−
1
{\displaystyle {\sqrt {x^{2}-1}}}
1
x
{\displaystyle {1 \over x}}
csc
1
x
{\displaystyle {1 \over x}}
1
1
−
x
2
{\displaystyle {1 \over {\sqrt {1-x^{2}}}}}
1
+
x
2
x
{\displaystyle {{\sqrt {1+x^{2}}} \over x}}
x
{\displaystyle x\ }
x
x
2
−
1
{\displaystyle {x \over {\sqrt {x^{2}-1}}}}
1
+
x
2
{\displaystyle {\sqrt {1+x^{2}}}}
sec
1
1
−
x
2
{\displaystyle {1 \over {\sqrt {1-x^{2}}}}}
1
x
{\displaystyle {1 \over x}}
1
+
x
2
{\displaystyle {\sqrt {1+x^{2}}}}
x
x
2
−
1
{\displaystyle {x \over {\sqrt {x^{2}-1}}}}
x
{\displaystyle x\ }
1
+
x
2
x
{\displaystyle {{\sqrt {1+x^{2}}} \over x}}
ctg
1
−
x
2
x
{\displaystyle {{\sqrt {1-x^{2}}} \over x}}
x
1
−
x
2
{\displaystyle {x \over {\sqrt {1-x^{2}}}}}
1
x
{\displaystyle {1 \over x}}
x
2
−
1
{\displaystyle {\sqrt {x^{2}-1}}}
1
x
2
−
1
{\displaystyle {1 \over {\sqrt {x^{2}-1}}}}
x
{\displaystyle x\ }
A táblázat függvénykompozíciók átalakítására is alkalmas. Adva legyen a φ és a ψ függvény, mivel egyenlő φ(arcψ(x ))?
A számítás módja:
Találjunk egy egyenletet, ami kapcsolatot teremt φ(u ) és ψ(u ) között.
f
(
φ
(
u
)
,
ψ
(
u
)
)
=
0
{\displaystyle f(\varphi (u),\psi (u))=0\ }
Legyen
u
=
arc
ψ
(
x
)
{\displaystyle u=\operatorname {arc} \psi (x)}
f
(
φ
(
a
r
c
ψ
(
x
)
)
,
x
)
=
0
{\displaystyle f(\varphi ({\rm {arc}}\psi (x)),x)=0\ }
Oldjuk meg ezt az egyenletet φ(arcψ(x ))-re. Példa: Mivel egyenlő ctg(arccsc(x ))?
Először kapcsolatot kell találnunk a ctg és a csc között.
c
t
g
2
u
+
1
=
csc
2
u
.
{\displaystyle \mathrm {ctg} ^{2}u+1=\csc ^{2}u\ .}
Másodszor végezzük el a következő helyettesítést: u = arccsc(x )
c
t
g
2
(
arccsc
(
x
)
)
+
1
=
csc
2
(
arccsc
(
x
)
)
{\displaystyle \mathrm {ctg} ^{2}(\operatorname {arccsc}(x))+1=\csc ^{2}(\operatorname {arccsc}(x))\ }
c
t
g
2
(
arccsc
(
x
)
)
+
1
=
x
2
.
{\displaystyle \mathrm {ctg} ^{2}(\operatorname {arccsc}(x))+1=x^{2}\ .}
Harmadszor oldjuk meg az egyenletet ctg(arccsc(x ))-re:
c
t
g
2
(
arccsc
(
x
)
)
=
x
2
−
1
,
{\displaystyle \mathrm {ctg} ^{2}(\operatorname {arccsc}(x))=x^{2}-1,\ }
c
t
g
(
arccsc
(
x
)
)
=
±
x
2
−
1
,
{\displaystyle \mathrm {ctg} (\operatorname {arccsc}(x))=\pm {\sqrt {x^{2}-1}},}
és ez az a képlet, ami a táblázat hatodik sorában és negyedik oszlopában van.
sin
(
∑
i
=
1
∞
ϑ
i
)
=
∑
p
a
r
a
t
l
a
n
k
≥
1
(
−
1
)
(
k
−
1
)
/
2
∑
A
⊆
{
1
,
2
,
3
,
…
}
|
A
|
=
k
(
∏
i
∈
A
sin
ϑ
i
∏
i
∉
A
cos
ϑ
i
)
{\displaystyle \sin \left(\sum _{i=1}^{\infty }\vartheta _{i}\right)=\sum _{\mathrm {paratlan} \ k\geq 1}(-1)^{(k-1)/2}\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}\left(\prod _{i\in A}\sin \vartheta _{i}\prod _{i\not \in A}\cos \vartheta _{i}\right)}
cos
(
∑
i
=
1
∞
ϑ
i
)
=
∑
p
a
r
o
s
k
≥
0
(
−
1
)
k
/
2
∑
A
⊆
{
1
,
2
,
3
,
…
}
|
A
|
=
k
(
∏
i
∈
A
sin
ϑ
i
∏
i
∉
A
cos
ϑ
i
)
{\displaystyle \cos \left(\sum _{i=1}^{\infty }\vartheta _{i}\right)=\sum _{\mathrm {paros} \ k\geq 0}~(-1)^{k/2}~~\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}\left(\prod _{i\in A}\sin \vartheta _{i}\prod _{i\not \in A}\cos \vartheta _{i}\right)}
Ezekben az azonosságokban megjelenik az az aszimmetria, ami a véges összegekben nincs meg: minden szorzatban véges sok szinuszos tényező van, és ko-véges koszinuszos.
Ha csak véges sok
ϑ
i
{\displaystyle \vartheta _{i}}
Legyen e k k -adfokú elemi szimmetrikus polinom , aminek változói x i θ i i = 1, ..., n , k = 0, ..., n .
Ekkor
t
g
(
θ
1
+
⋯
+
θ
n
)
=
e
1
−
e
3
+
e
5
−
⋯
e
0
−
e
2
+
e
4
−
⋯
,
{\displaystyle \mathrm {tg} (\theta _{1}+\cdots +\theta _{n})={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }},}
ahol a tagok száma n -től függ.
Például
t
g
(
θ
1
+
θ
2
+
θ
3
)
=
e
1
−
e
3
e
0
−
e
2
=
(
x
1
+
x
2
+
x
3
)
−
(
x
1
x
2
x
3
)
1
−
(
x
1
x
2
+
x
1
x
3
+
x
2
x
3
)
,
t
g
(
θ
1
+
θ
2
+
θ
3
+
θ
4
)
=
e
1
−
e
3
e
0
−
e
2
+
e
4
=
(
x
1
+
x
2
+
x
3
+
x
4
)
−
(
x
1
x
2
x
3
+
x
1
x
2
x
4
+
x
1
x
3
x
4
+
x
2
x
3
x
4
)
1
−
(
x
1
x
2
+
x
1
x
3
+
x
1
x
4
+
x
2
x
3
+
x
2
x
4
+
x
3
x
4
)
+
(
x
1
x
2
x
3
x
4
)
,
{\displaystyle {\begin{aligned}\mathrm {tg} (\theta _{1}+\theta _{2}+\theta _{3})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\\\\mathrm {tg} (\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\\\&{}={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}
Az általános eset teljes indukcióval bizonyítható.
sec
(
θ
1
+
⋯
+
θ
n
)
=
sec
θ
1
⋯
sec
θ
n
e
0
−
e
2
+
e
4
−
⋯
{\displaystyle \sec(\theta _{1}+\cdots +\theta _{n})={\frac {\sec \theta _{1}\cdots \sec \theta _{n}}{e_{0}-e_{2}+e_{4}-\cdots }}}
ahol e k k -adfokú elemi szimmetrikus polinom az x i θ i i = 1, ..., n , változókkal. A nevezőben levő tagok száma n -től függ.
Például
sec
(
α
+
β
+
γ
)
=
sec
α
sec
β
sec
γ
1
−
t
g
α
t
g
β
−
t
g
α
t
g
γ
−
t
g
β
t
g
γ
.
{\displaystyle \sec(\alpha +\beta +\gamma )={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\mathrm {tg} \alpha \mathrm {tg} \beta -\mathrm {tg} \alpha \mathrm {tg} \gamma -\mathrm {tg} \beta \mathrm {tg} \gamma }}.}
szerkesztés
Néhány könyvben találkozni lehet a
cis
(
x
)
=
cos
(
x
)
+
i
sin
(
x
)
,
{\displaystyle \operatorname {cis} (x)=\cos(x)+i\sin(x),\,}
jelöléssel, ahol a cis a "cos + i sin" függvény rövidítése.
Ez valójában az e ix exponenciális függvény .
A valós számok fölött értelmezett trigonometrikus függvények körében bizonyíthatók a következő azonosságok:
cos
(
x
+
y
)
=
cos
(
x
)
cos
(
y
)
−
sin
(
x
)
sin
(
y
)
=
c
1
c
2
−
s
1
s
2
,
{\displaystyle \cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)=c_{1}c_{2}-s_{1}s_{2},\,}
sin
(
x
+
y
)
=
sin
(
x
)
cos
(
y
)
+
cos
(
x
)
sin
(
y
)
=
s
1
c
2
+
c
1
s
2
.
{\displaystyle \sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y)=s_{1}c_{2}+c_{1}s_{2}.\,}
Hasonlóan, a komplex számokon bevezetve a szorzást megfigyelhető a trigonometria alkalmazása nélkül is:
c 1 + is 1 és c 2 + is 2 szorzatának valós és képzetes része rendre
c
1
c
2
−
s
1
s
2
,
{\displaystyle c_{1}c_{2}-s_{1}s_{2},\,}
s
1
c
2
+
c
1
s
2
.
{\displaystyle s_{1}c_{2}+c_{1}s_{2}.\,}
Ezek a hasonlóságok motiválják a két terület összekapcsolását és a trigonometrikus azonosság bizonyítását:
cis
(
x
+
y
)
=
cis
(
x
)
cis
(
y
)
,
{\displaystyle \operatorname {cis} (x+y)=\operatorname {cis} (x)\operatorname {cis} (y),\,}
ami egyszerűbb, mint a szinusz és a koszinusz összegzési képlete. Belátva ezt az azonosságot feltehető a kérdés, hogy mely függvények elégítik ki a
f
(
x
+
y
)
=
f
(
x
)
f
(
y
)
.
{\displaystyle f(x+y)=f(x)f(y).\,}
függvényegyenletet. Egy kis ellenőrzéssel belátható, hogy az exponenciális függvények ilyenek. Ez azt sugallja, hogy a cis függvény is exponenciális függvény, azaz felírható
cis
(
x
)
=
b
x
.
{\displaystyle \operatorname {cis} (x)=b^{x}.\,}
alakban egy b -re. Létezik-e ilyen b , és ha igen, akkor mivel egyenlő?
A cis függvény definíciója és a szinusz, koszinusz viselkedése a nulla közelében azt mutatja, hogy
cis
(
0
+
d
x
)
=
cis
(
0
)
+
i
d
x
,
{\displaystyle \operatorname {cis} (0+dx)=\operatorname {cis} (0)+i\,dx,}
azaz a cis függvény megváltozása a nulla közelében i , így az exponenciális függvény alapja e i
cis
(
x
)
=
e
i
x
.
{\displaystyle \operatorname {cis} (x)=e^{ix}.\,}
szerkesztés
A Gudermann-függvény anélkül teremt kapcsolatot a trigonometrikus és a hiperbolikus függvények között, hogy a komplex számokra hivatkozna.
Definíció: a Gudermann-függvényt így értelmezik:
g
d
(
x
)
=
∫
0
x
d
p
c
h
(
p
)
=
arcsin
(
t
g
h
(
x
)
)
=
arccsc
(
c
t
g
h
(
x
)
)
=
arccos
(
sech
x
)
)
=
arcsec
(
cosh
(
x
)
)
=
a
r
c
t
g
(
s
h
(
x
)
)
=
arcctg
(
csch
(
x
)
)
=
2
a
r
c
t
g
(
t
g
h
(
x
2
)
)
=
2
a
r
c
t
g
(
e
x
)
−
π
2
.
{\displaystyle {\begin{aligned}{\rm {gd}}(x)&=\int _{0}^{x}{\frac {dp}{\mathrm {ch} (p)}}\\&=\arcsin \left(\mathrm {tgh} (x)\right)={\mbox{arccsc}}\left(\mathrm {ctgh} (x)\right)\\&=\arccos \left({\mbox{sech}}x)\right)={\mbox{arcsec}}\left(\cosh(x)\right)\\&=\mathrm {arctg} \left(\mathrm {sh} (x)\right)={\mbox{arcctg}}\left({\mbox{csch}}(x)\right)\\&=2\mathrm {arctg} \left(\mathrm {tgh} \left({\frac {x}{2}}\right)\right)=2\mathrm {arctg} (e^{x})-{\frac {\pi }{2}}.\end{aligned}}\,\!}
Teljesülnek a következő azonosságok:
sin
(
gd
(
x
)
)
˙
=
tanh
(
x
)
;
csc
(
gd
(
x
)
)
=
c
t
g
h
(
x
)
;
cos
(
gd
(
x
)
)
=
sech
(
x
)
;
sec
(
gd
(
x
)
)
=
c
h
(
x
)
;
t
g
(
gd
(
x
)
)
=
sinh
(
x
)
;
c
t
g
(
gd
(
x
)
)
=
csch
(
x
)
;
.
t
g
(
gd
(
x
)
2
)
=
t
g
h
(
x
2
)
.
{\displaystyle {\begin{aligned}{\color {white}{\dot {\color {black}\sin({\mbox{gd}}(x))}}}&=\tanh(x);\quad \csc({\mbox{gd}}(x))=\mathrm {ctgh} (x);\\\cos({\mbox{gd}}(x))&={\mbox{sech}}(x);\quad \,\sec({\mbox{gd}}(x))=\mathrm {ch} (x);\\\mathrm {tg} ({\mbox{gd}}(x))&=\sinh(x);\quad \,\mathrm {ctg} ({\mbox{gd}}(x))={\mbox{csch}}(x);\\{}_{\color {white}.}\mathrm {tg} \left({\frac {{\mbox{gd}}(x)}{2}}\right)&=\mathrm {tgh} \left({\frac {x}{2}}\right).\end{aligned}}\,\!}
A Gudermann-függvény inverze:
arcgd
(
x
)
=
g
d
−
1
(
x
)
=
∫
0
x
d
p
cos
(
p
)
=
arcch
(
sec
(
x
)
)
=
arctgh
(
sin
(
x
)
)
=
ln
(
sec
(
x
)
(
1
+
sin
(
x
)
)
)
=
ln
(
t
g
(
x
)
+
sec
(
x
)
)
=
ln
t
g
(
π
4
+
x
2
)
=
1
2
ln
1
+
sin
(
x
)
1
−
sin
(
x
)
.
{\displaystyle {\begin{aligned}{\mbox{arcgd}}(x)&={\rm {gd}}^{-1}(x)=\int _{0}^{x}{\frac {dp}{\cos(p)}}\\&={}{\mbox{arcch}}(\sec(x))={\mbox{arctgh}}(\sin(x))\\&={}\ln \left(\sec(x)(1+\sin(x))\right)\\&={}\ln(\mathrm {tg} (x)+\sec(x))=\ln \mathrm {tg} \left({\frac {\pi }{4}}+{\frac {x}{2}}\right)\\&={}{\frac {1}{2}}\ln {\frac {1+\sin(x)}{1-\sin(x)}}.\end{aligned}}\,\!}
A Gudermann-függvény és inverzének deriváltjai:
d
d
x
gd
(
x
)
=
sech
(
x
)
;
d
d
x
arcgd
(
x
)
=
sec
(
x
)
.
{\displaystyle {\frac {d}{dx}}\;{\mbox{gd}}(x)={\mbox{sech}}(x);\quad {\frac {d}{dx}}\;{\mbox{arcgd}}(x)=\sec(x).\,\!}
Az érdekes
cos
20
∘
⋅
cos
40
∘
⋅
cos
80
∘
=
1
8
{\displaystyle \cos 20^{\circ }\cdot \cos 40^{\circ }\cdot \cos 80^{\circ }={\frac {1}{8}}}
azonosság a következő egy változót tartalmazó azonosság speciális esete:
∏
j
=
0
k
−
1
cos
(
2
j
x
)
=
sin
(
2
k
x
)
2
k
sin
(
x
)
.
{\displaystyle \prod _{j=0}^{k-1}\cos(2^{j}x)={\frac {\sin(2^{k}x)}{2^{k}\sin(x)}}.}
Hasonló a
cos
π
7
cos
2
π
7
cos
3
π
7
=
1
8
.
{\displaystyle \cos {\frac {\pi }{7}}\cos {\frac {2\pi }{7}}\cos {\frac {3\pi }{7}}={\frac {1}{8}}.}
A következő azonosság talán nem is általánosítható:
cos
24
∘
+
cos
48
∘
+
cos
96
∘
+
cos
168
∘
=
1
2
.
{\displaystyle \cos 24^{\circ }+\cos 48^{\circ }+\cos 96^{\circ }+\cos 168^{\circ }={\frac {1}{2}}.}
A szögeket célszerűbb a következő azonosságban radiánban mérni:
cos
(
2
π
21
)
+
cos
(
2
⋅
2
π
21
)
+
cos
(
4
⋅
2
π
21
)
{\displaystyle \cos \left({\frac {2\pi }{21}}\right)\,+\,\cos \left(2\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(4\cdot {\frac {2\pi }{21}}\right)}
+
cos
(
5
⋅
2
π
21
)
+
cos
(
8
⋅
2
π
21
)
+
cos
(
10
⋅
2
π
21
)
=
1
2
.
{\displaystyle \,+\,\cos \left(5\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(8\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(10\cdot {\frac {2\pi }{21}}\right)={\frac {1}{2}}.}
Az 1, 2, 4, 5, 8, és a 10 tiszta mintát mutat: ezek azok a 21/2-nél kisebb egész számok , amelyek relatív prímek 21-hez. A legutóbbi példa a felbonthatatlan körosztási polinomokhoz kapcsolódnak: a koszinuszok valós részei a körosztási polinomok gyökeinek. A gyökök összege egyenlő a Möbius-függvény 21-ben vett helyettesítési értékével. Az előtte levő két példa 21 helyett 10-zel és 15-tel kapható.
A pí szám kiszámításának egy John Machin által talált hatékony módja:
π
4
=
4
a
r
c
t
g
1
5
−
a
r
c
t
g
1
239
{\displaystyle {\frac {\pi }{4}}=4\mathrm {arctg} {\frac {1}{5}}-\mathrm {arctg} {\frac {1}{239}}}
vagy az Euler-formulával:
π
4
=
5
a
r
c
t
g
1
7
+
2
a
r
c
t
g
3
79
.
{\displaystyle {\frac {\pi }{4}}=5\mathrm {arctg} {\frac {1}{7}}+2\mathrm {arctg} {\frac {3}{79}}.}
sin
0
=
sin
0
∘
=
0
=
cos
90
∘
=
cos
(
π
2
)
sin
(
π
6
)
=
sin
30
∘
=
1
/
2
=
cos
60
∘
=
cos
(
π
3
)
sin
(
π
4
)
=
sin
45
∘
=
2
/
2
=
cos
45
∘
=
cos
(
π
4
)
sin
(
π
3
)
=
sin
60
∘
=
3
/
2
=
cos
30
∘
=
cos
(
π
6
)
sin
(
π
2
)
=
sin
90
∘
=
1
=
cos
0
∘
=
cos
0
{\displaystyle {\begin{matrix}\sin 0&=&\sin 0^{\circ }&=&0&=&\cos 90^{\circ }&=&\cos \left({\frac {\pi }{2}}\right)\\\\\sin \left({\frac {\pi }{6}}\right)&=&\sin 30^{\circ }&=&1/2&=&\cos 60^{\circ }&=&\cos \left({\frac {\pi }{3}}\right)\\\\\sin \left({\frac {\pi }{4}}\right)&=&\sin 45^{\circ }&=&{\sqrt {2}}/2&=&\cos 45^{\circ }&=&\cos \left({\frac {\pi }{4}}\right)\\\\\sin \left({\frac {\pi }{3}}\right)&=&\sin 60^{\circ }&=&{\sqrt {3}}/2&=&\cos 30^{\circ }&=&\cos \left({\frac {\pi }{6}}\right)\\\\\sin \left({\frac {\pi }{2}}\right)&=&\sin 90^{\circ }&=&1&=&\cos 0^{\circ }&=&\cos 0\end{matrix}}}
sin
π
7
=
7
6
−
7
189
∑
j
=
0
∞
(
3
j
+
1
)
!
189
j
j
!
(
2
j
+
2
)
!
{\displaystyle \sin {\frac {\pi }{7}}={\frac {\sqrt {7}}{6}}-{\frac {\sqrt {7}}{189}}\sum _{j=0}^{\infty }{\frac {(3j+1)!}{189^{j}j!\,(2j+2)!}}\!}
sin
π
18
=
1
6
∑
j
=
0
∞
(
3
j
)
!
27
j
j
!
(
2
j
+
1
)
!
{\displaystyle \sin {\frac {\pi }{18}}={\frac {1}{6}}\sum _{j=0}^{\infty }{\frac {(3j)!}{27^{j}j!\,(2j+1)!}}\!}
A φ aranymetszési számmal:
cos
(
π
5
)
=
cos
36
∘
=
5
+
1
4
=
φ
/
2
{\displaystyle \cos \left({\frac {\pi }{5}}\right)=\cos 36^{\circ }={{\sqrt {5}}+1 \over 4}=\varphi /2}
sin
(
π
10
)
=
sin
18
∘
=
5
−
1
4
=
φ
−
1
2
=
1
2
φ
{\displaystyle \sin \left({\frac {\pi }{10}}\right)=\sin 18^{\circ }={{\sqrt {5}}-1 \over 4}={\varphi -1 \over 2}={1 \over 2\varphi }}
Ezek a bizonyítások közvetlenül csak hegyesszögekre alkalmazhatók, de az azonosságok minden szögre teljesülnek. Így a legtöbb trigonometriai azonosság levezethető elemi geometriai úton, bár a definíciókat és az elgondolásokat ki kell terjeszteni.
A mellékelt ábrán az x szög a derékszögű ABC háromszöghöz, és az y szög a derékszögű ACD háromszöghöz tartozik. Szerkesszük meg az AB oldalra merőleges DG, és az AB oldallal párhuzamos CE szakaszt.
Ekkor teljesülnek a következők:
x = BAC = ACE = CDE
és
EG = BC.
sin
(
x
+
y
)
{\displaystyle \sin(x+y)\,}
=
D
G
A
D
{\displaystyle ={\frac {DG}{AD}}\,}
=
E
G
+
D
E
A
D
{\displaystyle ={\frac {EG+DE}{AD}}\,}
=
B
C
+
D
E
A
D
{\displaystyle ={\frac {BC+DE}{AD}}\,}
=
B
C
A
D
+
D
E
A
D
{\displaystyle ={\frac {BC}{AD}}+{\frac {DE}{AD}}\,}
=
B
C
A
D
⋅
A
C
A
C
+
D
E
A
D
⋅
C
D
C
D
{\displaystyle ={\frac {BC}{AD}}\cdot {\frac {AC}{AC}}+{\frac {DE}{AD}}\cdot {\frac {CD}{CD}}\,}
=
B
C
A
C
⋅
A
C
A
D
+
D
E
C
D
⋅
C
D
A
D
{\displaystyle ={\frac {BC}{AC}}\cdot {\frac {AC}{AD}}+{\frac {DE}{CD}}\cdot {\frac {CD}{AD}}\,}
=
sin
(
x
)
cos
(
y
)
+
cos
(
x
)
sin
(
y
)
.
{\displaystyle =\sin(x)\cos(y)+\cos(x)\sin(y).\,}
A fenti ábra alapján:
cos
(
x
+
y
)
{\displaystyle \cos(x+y)\,}
=
A
G
A
D
{\displaystyle ={\frac {AG}{AD}}\,}
=
A
B
−
G
B
A
D
{\displaystyle ={\frac {AB-GB}{AD}}\,}
=
A
B
−
E
C
A
D
{\displaystyle ={\frac {AB-EC}{AD}}\,}
=
A
B
A
D
−
E
C
A
D
{\displaystyle ={\frac {AB}{AD}}-{\frac {EC}{AD}}\,}
=
A
B
A
D
⋅
A
C
A
C
−
E
C
A
D
⋅
C
D
C
D
{\displaystyle ={\frac {AB}{AD}}\cdot {\frac {AC}{AC}}-{\frac {EC}{AD}}\cdot {\frac {CD}{CD}}\,}
=
A
B
A
C
⋅
A
C
A
D
−
E
C
C
D
⋅
C
D
A
D
{\displaystyle ={\frac {AB}{AC}}\cdot {\frac {AC}{AD}}-{\frac {EC}{CD}}\cdot {\frac {CD}{AD}}\,}
=
cos
(
x
)
cos
(
y
)
−
sin
(
x
)
sin
(
y
)
.
{\displaystyle =\cos(x)\cos(y)-\sin(x)\sin(y).\,}
Ezek az azonosságok könnyen bizonyíthatók a cos(x + y ) és a sin(x + y ) azonosságok felhasználásával:
Először is írjunk y helyett -y -t.
sin
(
x
+
(
−
y
)
)
=
sin
(
x
)
cos
(
−
y
)
+
cos
(
x
)
sin
(
−
y
)
.
{\displaystyle \!\sin(x+(-y))=\sin(x)\cos(-y)+\cos(x)\sin(-y).}
A szinusz páratlan, és a koszinusz páros függvény, így
sin
(
x
−
y
)
=
sin
(
x
)
cos
(
y
)
−
cos
(
x
)
sin
(
y
)
.
{\displaystyle \!\sin(x-y)=\sin(x)\cos(y)-\cos(x)\sin(y).}
Először is írjunk y helyett -y -t cos(x + y )-ben:
cos
(
x
+
(
−
y
)
)
=
cos
(
x
)
cos
(
−
y
)
−
sin
(
x
)
sin
(
−
y
)
.
{\displaystyle \!\cos(x+(-y))=\cos(x)\cos(-y)-\sin(x)\sin(-y).}
A szinusz páratlan, és a koszinusz páros függvény, így
cos
(
x
−
y
)
=
cos
(
x
)
cos
(
y
)
+
sin
(
x
)
sin
(
y
)
.
{\displaystyle \!\cos(x-y)=\cos(x)\cos(y)+\sin(x)\sin(y).}
Az analízisben a szögeket radiánban mérik, így a képletek egyszerűbbekké válnak.
A trigonometrikus függvények deriváltjainak meghatározásához két határérték szükséges.
Ezek egyike:
lim
x
→
0
sin
x
x
=
1
,
{\displaystyle \lim _{x\rightarrow 0}{\frac {\sin x}{x}}=1,}
az egységsugarú kör tulajdonságai és a rendőrelv segítségével bizonyítható. Csábító az ötlet, hogy a L'Hôpital-szabályt alkalmazzuk, de ez körben forgó okoskodáshoz vezetne. Ugyanis ezt a határértéket használják arra, hogy belássák, a szinusz deriváltja koszinusz, és ezzel az utóbbival vezetik le a L'Hôpital-szabályt.
A második határérték:
lim
x
→
0
1
−
cos
x
x
=
0
,
{\displaystyle \lim _{x\rightarrow 0}{\frac {1-\cos x}{x}}=0,}
a tg(x /2) = (1 ‒ cos(x ))/sin(x ) azonosság felhasználásával igazolható.
A két határérték segítségével, a derivált határértékes definíciójával és az összegzési képletekkel megmutatható, hogy sin′(x ) = cos(x ) and cos′(x ) = ‒sin(x ).
Ha a szinusz és a koszinusz Taylor-sorukkal van definiálva, akkor deriváltjukat a hatványsor tagonkénti deriválásával lehet megkapni.
d
d
x
sin
(
x
)
=
cos
(
x
)
{\displaystyle {d \over dx}\sin(x)=\cos(x)}
A többi trigonometrikus függvény deriváltja a fenti azonosságok és a deriválás szabályai alapján határozhatók meg.
d
d
x
sin
x
=
cos
x
,
d
d
x
arcsin
x
=
1
1
−
x
2
d
d
x
cos
x
=
−
sin
x
,
d
d
x
arccos
x
=
−
1
1
−
x
2
d
d
x
t
g
x
=
sec
2
x
,
d
d
x
a
r
c
t
g
x
=
1
1
+
x
2
d
d
x
c
t
g
x
=
−
csc
2
x
,
d
d
x
a
r
c
c
t
g
x
=
−
1
1
+
x
2
d
d
x
sec
x
=
t
g
x
sec
x
,
d
d
x
arcsec
x
=
1
|
x
|
x
2
−
1
d
d
x
csc
x
=
−
csc
x
c
t
g
x
,
d
d
x
arccsc
x
=
−
1
|
x
|
x
2
−
1
{\displaystyle {\begin{matrix}{d \over dx}\sin x=&\cos x,&{d \over dx}\arcsin x=&{1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\cos x=&-\sin x,&{d \over dx}\arccos x=&{-1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\mathrm {tg} x=&\sec ^{2}x,&{d \over dx}\mathrm {arctg} x=&{1 \over 1+x^{2}}\\\\{d \over dx}\mathrm {ctg} x=&-\csc ^{2}x,&{d \over dx}\mathrm {arcctg} x=&{-1 \over 1+x^{2}}\\\\{d \over dx}\sec x=&\mathrm {tg} x\sec x,&{d \over dx}\operatorname {arcsec} x=&{1 \over |x|{\sqrt {x^{2}-1}}}\\\\{d \over dx}\csc x=&-\csc x\mathrm {ctg} x,&{d \over dx}\operatorname {arccsc} x=&{-1 \over |x|{\sqrt {x^{2}-1}}}\end{matrix}}}
A szinusz és a koszinusz lineáris kombinációinak deriváltjai a szinusz és a koszinusz lineáris kombinációinak deriváltjai. Ez alapvető fontosságú a matematika több területén is, így például a differenciálegyenletekben és a Fourier-transzformációkban .
szerkesztés
sin
(
θ
)
=
e
i
θ
−
e
−
i
θ
2
i
{\displaystyle \sin(\theta )={\frac {e^{i\theta }-e^{-i\theta }}{2i}}\,}
cos
(
θ
)
=
e
i
θ
+
e
−
i
θ
2
{\displaystyle \cos(\theta )={\frac {e^{i\theta }+e^{-i\theta }}{2}}\,}
t
g
(
θ
)
=
sin
(
θ
)
cos
(
θ
)
=
(
e
i
θ
−
e
−
i
θ
2
i
)
(
e
i
θ
+
e
−
i
θ
2
)
{\displaystyle \mathrm {tg} (\theta )={\frac {\sin(\theta )}{\operatorname {cos} (\theta )}}={\frac {({\frac {e^{i\theta }-e^{-i\theta }}{2i}})}{({\frac {e^{i\theta }+e^{-i\theta }}{2}})}}\,}
c
t
g
(
θ
)
=
cos
(
θ
)
sin
(
θ
)
=
(
e
i
θ
+
e
−
i
θ
2
)
(
e
i
θ
−
e
−
i
θ
2
i
)
{\displaystyle \mathrm {ctg} (\theta )={\frac {\cos(\theta )}{\sin(\theta )}}={\frac {({\frac {e^{i\theta }+e^{-i\theta }}{2}})}{({\frac {e^{i\theta }-e^{-i\theta }}{2i}})}}\,}
sec
(
θ
)
=
1
cos
(
θ
)
=
1
(
e
i
θ
+
e
−
i
θ
2
)
{\displaystyle \sec(\theta )={\frac {1}{\cos(\theta )}}={\frac {1}{({\frac {e^{i\theta }+e^{-i\theta }}{2}})}}\,}
csc
(
θ
)
=
1
sin
(
θ
)
=
1
(
e
i
θ
−
e
−
i
θ
2
i
)
{\displaystyle \csc(\theta )={\frac {1}{\sin(\theta )}}={\frac {1}{({\frac {e^{i\theta }-e^{-i\theta }}{2i}})}}\,}
versin
(
θ
)
=
1
−
cos
(
θ
)
=
1
−
e
i
θ
+
e
−
i
θ
2
{\displaystyle \operatorname {versin} (\theta )=1-\cos(\theta )=1-{\frac {e^{i\theta }+e^{-i\theta }}{2}}\,}
vercos
(
θ
)
=
1
−
sin
(
θ
)
=
1
−
e
i
θ
−
e
−
i
θ
2
i
{\displaystyle \operatorname {vercos} (\theta )=1-\sin(\theta )=1-{\frac {e^{i\theta }-e^{-i\theta }}{2i}}\,}
exsec
(
θ
)
=
sec
(
θ
)
−
1
=
1
cos
(
θ
)
−
1
=
1
(
e
i
θ
+
e
−
i
θ
2
)
−
1
{\displaystyle \operatorname {exsec} (\theta )=\operatorname {sec} (\theta )-1\ ={\frac {1}{\cos(\theta )}}-1={\frac {1}{({\frac {e^{i\theta }+e^{-i\theta }}{2}})}}-1\,}
excsc
(
θ
)
=
csc
(
θ
)
−
1
=
1
sin
(
θ
)
−
1
=
1
(
e
i
θ
−
e
−
i
θ
2
i
)
−
1
{\displaystyle \operatorname {excsc} (\theta )=\operatorname {csc} (\theta )-1\ ={\frac {1}{\sin(\theta )}}-1={\frac {1}{({\frac {e^{i\theta }-e^{-i\theta }}{2i}})}}-1\,}
s
h
(
θ
)
=
−
i
sin
(
i
θ
)
=
e
θ
−
e
−
θ
2
{\displaystyle \mathrm {sh} (\theta )=-i\sin(i\theta )={\frac {e^{\theta }-e^{-\theta }}{2}}\,}
c
h
(
θ
)
=
cos
(
i
θ
)
=
e
θ
+
e
−
θ
2
{\displaystyle \mathrm {ch} (\theta )=\cos(i\theta )={\frac {e^{\theta }+e^{-\theta }}{2}}\,}
t
g
h
(
θ
)
=
−
i
t
g
(
i
θ
)
=
sh
(
θ
)
ch
(
θ
)
=
e
θ
−
e
−
θ
e
θ
+
e
−
θ
=
e
2
θ
−
1
e
2
θ
+
1
{\displaystyle \mathrm {tgh} (\theta )=-i\mathrm {tg} (i\theta )={\frac {\operatorname {sh} (\theta )}{\operatorname {ch} (\theta )}}={\frac {e^{\theta }-e^{-\theta }}{e^{\theta }+e^{-\theta }}}={\frac {e^{2\theta }-1}{e^{2\theta }+1}}\,}
c
t
g
h
(
θ
)
=
i
cot
(
i
θ
)
=
ch
(
θ
)
sh
(
θ
)
=
e
θ
+
e
−
θ
e
θ
−
e
−
θ
=
e
2
θ
+
1
e
2
θ
−
1
{\displaystyle \mathrm {ctgh} (\theta )=i\operatorname {cot} (i\theta )={\frac {\operatorname {ch} (\theta )}{\operatorname {sh} (\theta )}}={\frac {e^{\theta }+e^{-\theta }}{e^{\theta }-e^{-\theta }}}={\frac {e^{2\theta }+1}{e^{2\theta }-1}}\,}
sech
(
θ
)
=
1
ch
(
θ
)
=
sec
(
i
θ
)
=
2
e
θ
+
e
−
θ
{\displaystyle \operatorname {sech} (\theta )={\frac {1}{\operatorname {ch} (\theta )}}=\operatorname {sec} (i\theta )={\frac {2}{e^{\theta }+e^{-\theta }}}\,}
csch
(
θ
)
=
1
sh
(
θ
)
=
i
cos
(
i
θ
)
=
2
e
θ
−
e
−
θ
{\displaystyle \operatorname {csch} (\theta )={\frac {1}{\operatorname {sh} (\theta )}}=i\cos(i\theta )={\frac {2}{e^{\theta }-e^{-\theta }}}\,}
v
e
r
s
h
(
θ
)
=
1
−
cos
(
i
θ
)
=
1
−
e
θ
+
e
−
θ
2
{\displaystyle \mathrm {versh} (\theta )=1-\cos(i\theta )=1-{\frac {e^{\theta }+e^{-\theta }}{2}}\,}
v
e
r
c
h
(
θ
)
=
1
+
i
sin
(
i
θ
)
=
1
−
e
θ
−
e
−
θ
2
{\displaystyle \mathrm {verch} (\theta )=1+i\sin(i\theta )=1-{\frac {e^{\theta }-e^{-\theta }}{2}}\,}
exsech
(
θ
)
=
sech
(
θ
)
−
1
=
1
ch
(
θ
)
−
1
=
sec
(
i
θ
)
=
2
e
θ
+
e
−
θ
−
1
{\displaystyle \operatorname {exsech} (\theta )=\operatorname {sech} (\theta )-1={\frac {1}{\operatorname {ch} (\theta )}}-1=\operatorname {sec} (i\theta )={\frac {2}{e^{\theta }+e^{-\theta }}}-1\,}
excsch
(
θ
)
=
csch
(
θ
)
−
1
=
1
sh
(
θ
)
−
1
=
i
cos
(
i
θ
)
=
2
e
θ
−
e
−
θ
−
1
{\displaystyle \operatorname {excsch} (\theta )=\operatorname {csch} (\theta )-1={\frac {1}{\operatorname {sh} (\theta )}}-1=i\cos(i\theta )={\frac {2}{e^{\theta }-e^{-\theta }}}-1\,}
arcsin
(
θ
)
=
−
i
ln
(
i
θ
+
1
−
θ
2
)
{\displaystyle \arcsin(\theta )=-i\ln(i\theta +{\sqrt {1-\theta ^{2}}})\,}
arccos
(
θ
)
=
−
i
ln
(
θ
+
i
1
−
θ
2
)
{\displaystyle \arccos(\theta )=-i\ln(\theta +i{\sqrt {1-\theta ^{2}}})\,}
a
r
c
t
g
(
θ
)
=
ln
(
i
+
θ
i
−
θ
)
i
2
{\displaystyle \mathrm {arctg} (\theta )={\frac {\ln({\frac {i+\theta }{i-\theta }})i}{2}}\,}
a
r
c
c
t
g
θ
)
=
arctan
(
−
θ
)
=
i
ln
(
i
−
θ
i
+
θ
)
2
{\displaystyle \mathrm {arcctg} \theta )=\arctan(-\theta )={\frac {i\ln({\frac {i-\theta }{i+\theta }})}{2}}\,}
arcsec
(
θ
)
=
arccos
(
θ
−
1
)
=
−
i
ln
(
θ
−
1
+
1
−
θ
−
2
i
)
{\displaystyle \operatorname {arcsec}(\theta )=\arccos(\theta ^{-1})=-i\ln(\theta ^{-1}+{\sqrt {1-\theta ^{-2}}}i)\,}
arccsc
(
θ
)
=
arcsin
(
θ
−
1
)
=
−
i
ln
(
i
θ
−
1
+
1
−
θ
−
2
)
{\displaystyle \operatorname {arccsc}(\theta )=\arcsin(\theta ^{-1})=-i\ln(i\theta ^{-1}+{\sqrt {1-\theta ^{-2}}})\,}
arcversin
(
θ
)
=
arccos
(
1
−
θ
)
=
−
i
ln
(
1
−
θ
+
i
1
−
(
1
−
θ
)
2
)
{\displaystyle \operatorname {arcversin} (\theta )=\arccos(1-\theta )=-i\ln(1-\theta +i{\sqrt {1-(1-\theta )^{2}}})\,}
arcvercos
(
θ
)
=
arcsin
(
1
−
θ
)
=
−
i
ln
(
i
−
i
θ
+
1
−
(
1
−
θ
)
2
)
{\displaystyle \operatorname {arcvercos} (\theta )=\operatorname {arcsin} (1-\theta )=-i\ln(i-i\theta +{\sqrt {1-(1-\theta )^{2}}})\,}
arcexsec
(
θ
)
=
arcsec
(
1
+
θ
)
=
−
i
ln
(
(
θ
+
1
)
−
1
+
i
1
−
(
1
+
θ
)
2
)
{\displaystyle \operatorname {arcexsec} (\theta )=\operatorname {arcsec}(1+\theta )=-i\ln((\theta +1)^{-1}+i{\sqrt {1-(1+\theta )^{2}}})\,}
arcexcsc
(
θ
)
=
arccsc
(
1
+
θ
)
=
−
i
ln
(
i
(
θ
+
1
)
−
1
+
1
−
(
1
+
θ
)
2
)
{\displaystyle \operatorname {arcexcsc} (\theta )=\operatorname {arccsc}(1+\theta )=-i\ln(i(\theta +1)^{-1}+{\sqrt {1-(1+\theta )^{2}}})\,}
a
r
c
s
h
(
θ
)
=
ln
(
θ
+
θ
2
+
1
)
{\displaystyle \mathrm {arcsh} (\theta )=\ln(\theta +{\sqrt {\theta ^{2}+1}})\,}
a
r
c
c
h
(
θ
)
=
ln
(
θ
+
θ
2
−
1
)
{\displaystyle \mathrm {arcch} (\theta )=\ln(\theta +{\sqrt {\theta ^{2}-1}})\,}
a
r
c
t
g
h
(
θ
)
=
ln
(
i
+
θ
i
−
θ
)
2
{\displaystyle \mathrm {arctgh} (\theta )={\frac {\ln({\frac {i+\theta }{i-\theta }})}{2}}\,}
a
r
c
c
t
g
h
(
θ
)
=
arctgh
(
−
θ
)
=
ln
(
i
−
θ
i
+
θ
)
2
{\displaystyle \mathrm {arcctgh} (\theta )=\operatorname {arctgh} (-\theta )={\frac {\ln({\frac {i-\theta }{i+\theta }})}{2}}\,}
arcsech
(
θ
)
=
arcch
(
θ
−
1
)
=
ln
(
θ
−
1
+
θ
−
2
−
1
)
{\displaystyle \operatorname {arcsech} (\theta )=\operatorname {arcch} (\theta ^{-1})=\ln(\theta ^{-1}+{\sqrt {\theta ^{-2}-1}})\,}
arccsch
(
θ
)
=
arcsh
(
θ
−
1
)
=
ln
(
θ
−
1
+
θ
−
2
+
1
)
{\displaystyle \operatorname {arccsch} (\theta )=\operatorname {arcsh} (\theta ^{-1})=\ln(\theta ^{-1}+{\sqrt {\theta ^{-2}+1}})\,}
a
r
c
v
e
r
s
h
(
θ
)
=
arcch
(
θ
)
−
1
=
ln
(
θ
+
θ
2
−
1
)
−
1
{\displaystyle \mathrm {arcversh} (\theta )=\operatorname {arcch} (\theta )-1=\ln(\theta +{\sqrt {\theta ^{2}-1}})-1\,}
a
r
c
v
e
r
c
h
(
θ
)
=
arcsh
(
θ
)
−
1
=
ln
(
θ
+
θ
2
+
1
)
−
1
{\displaystyle \mathrm {arcverch} (\theta )=\operatorname {arcsh} (\theta )-1=\ln(\theta +{\sqrt {\theta ^{2}+1}})-1\,}
arcexsech
(
θ
)
=
arcsech
(
θ
+
1
)
=
arcch
(
(
θ
+
1
)
−
1
)
=
ln
(
(
θ
+
1
)
−
1
+
(
θ
+
1
)
−
2
−
1
)
{\displaystyle \operatorname {arcexsech} (\theta )=\operatorname {arcsech} (\theta +1)=\operatorname {arcch} ((\theta +1)^{-1})=\ln((\theta +1)^{-1}+{\sqrt {(\theta +1)^{-2}-1}})\,}
arcexcsch
(
θ
)
=
arccsch
(
θ
+
1
)
=
arcsh
(
(
θ
+
1
)
−
1
)
=
ln
(
(
θ
+
1
)
−
1
+
(
θ
+
1
)
−
2
+
1
)
{\displaystyle \operatorname {arcexcsch} (\theta )=\operatorname {arccsch} (\theta +1)=\operatorname {arcsh} ((\theta +1)^{-1})=\ln((\theta +1)^{-1}+{\sqrt {(\theta +1)^{-2}+1}})\,}