Hadwiger-szám

A matematika, azon belül a gráfelmélet területén egy G irányítatlan gráf Hadwiger-száma annak a legnagyobb teljes gráfnak a mérete, ami G éleinek összehúzásával előállítható. Ezzel ekvivalens megfogalmazás szerint a h(G) Hadwiger-szám megegyezik annak a legnagyobb K_k teljes gráfnak a k méretével, ami G-nek minora, azaz előállítható belőle az élösszehúzás, csúcstörlés és éltörlés műveletek segítségével. Úgy is ismert, mint G összehúzási klikkszáma (contraction clique number) vagy G homomorfizmus-foka (homomorphism degree). Nevét Hugo Hadwigerről kapta, aki 1943-ban a Hadwiger-sejtés kapcsán bevezette; a sejtés állítása szerint a Hadwiger-szám minden esetben legalább akkora, mint G kromatikus száma.

Egy gráf négy összefüggő részgráffal, melyek összehúzásával teljes gráf jön létre. A Wagner-tétel értelmében nincs ötcsúcsú teljes minora, ezért Hadwiger-száma pontosan négy.

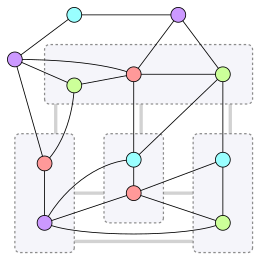
A legfeljebb négy Hadwiger-számú gráfok jellemzését (Wagner 1937) végezte el. A korlátos Hadwiger-számú gráfok ritkák, kromatikus számuk alacsony. Egy gráf Hadwiger-számának megállapítása NP-nehéz, de rögzített paraméter mellett kezelhető.

Alacsony Hadwiger-számú gráfok

Egy G gráf Hadwiger-száma pontosan akkor legfeljebb kettő, ha az fa vagy erdő, mivel egy három csúcs alkotta teljes minor csak egy G-beli kör összehúzásával jöhet létre.

Egy gráf Hadwiger-száma pontosan akkor legfeljebb három, ha favastagsága legfeljebb kettő, ami akkor és csak akkor igaz, ha minden kétszeresen összefüggő komponense soros-párhuzamos gráf.

Két síkbarajzolható gráf és a Wagner-gráf klikkösszege egy négy Hadwiger-számú nagyobb gráf lesz.

A síkbarajzolható gráfokat tiltott minoraik alapján jellemző Wagner-tétel alapján a síkbarajzolható gráfok Hadwiger-száma legfeljebb négy. Ugyanabban a cikkben, amiben a tételt is bizonyította, (Wagner 1937) elvégezte a legfeljebb négy Hadwiger-számú gráfok precízebb jellemzését is: ezek a gráfok, melyek létrehozhatók a nyolc csúcsú Wagner-gráfból és síkbarajzolható gráfokból a klikk-összeg művelet segítségével.

A legfeljebb öt Hadwiger-számú gráfok közé tartoznak a csúcsgráfok és a láncmentesen beágyazható gráfok, melyek közül mindkettőnek a tiltott minorai között szerepel a K₆ teljes gráf.

Ritkaság

Bármely, n csúcsú és k Hadwiger-számú gráf éleinek száma O(nk √log k). Ez a korlát éles: minden k értékre létezik olyan, k Hadwiger-számú gráf, melyben Ω(nk √log k) él van. Ha a G gráf Hadwiger-száma k, akkor minden részgráfjára igaz, hogy Hadwiger-száma legfeljebb k, amiből következik, hogy G degeneráltsága O(k √log k). Ezért a korlátos Hadwiger-számú gráfok ritka gráfok.

Színezés

A Hadwiger-sejtés szerint a Hadwiger-szám legalább akkora, mint az adott gráf kromatikus száma. Tehát minden k Hadwiger-számú gráfnak kellene lennie legfeljebb k színt használó színezésének. A k = 4 eset (Wagner a 4-es Hadwiger-számú gráfokkal foglalkozó jellemzése alapján) ekvivalens a síkbarajzolható gráfokra vonatkozó négyszíntétellel, és a sejtést k ≤ 5-re bizonyították is, de k nagyobb értékeire nem ismert, hogy igaz-e.

Alacsony degeneráltsági értékük miatt a legfeljebb k Hadwiger-számú gráfok mohó színezési algoritmussal O(k √log k) színnel színezhetők.

Számítási bonyolultság

Annak tesztelése, hogy egy konkrét gráf Hadwiger-száma elér-e egy adott k értéket NP-teljes feladat, amiből következik, hogy a Hadwiger-szám meghatározása NP-nehéz. A probléma azonban rögzített paraméter mellett kezelhető: létezik a legnagyobb klikkminor megkeresésére szolgáló algoritmus, aminek futási ideje a gráf méretének polinom, h(G)-nek pedig exponenciális függvénye. Ráadásul polinom idejű algoritmusokkal lényegesen jobban (pontosabban) közelíthető a Hadwiger-szám, mint a legnagyobb teljes részgráf keresésére szolgáló legjobb polinom idejű approximáció (feltéve, hogy P ≠ NP).

Kapcsolódó fogalmak

Egy G gráf akromatikus száma a legnagyobb klikkjének mérete, ami előállítható G független csúcshalmazai egy családjának összehúzásával.

Végtelen gráfok megszámlálhatatlan klikkminorai jellemezhetők a bennük található menedékekkel, melyek az üldözős-menekülős játékok elkerülő stratégiáit formalizálják: ha a Hadwiger-szám nem megszámlálható, akkor megegyezik a gráf menedékei közül a legnagyobb rendűvel.

Bármely k Hadwiger-számú gráfnak legfeljebb n2^{O(k log log k)} klikkje (teljes részgráfja) lehet.

(Halin 1976) egy S-függvények nevű gráfparaméter-osztályt definiál, melybe a Hadwiger-szám is beletartozik. Ezeknek a gráfokhoz egész számokat rendelő függvényeknek a következő tulajdonságokkal kell rendelkezniük: az üres gráfon legyen nulla az értékük, legyenek minor-monotonok, értékük eggyel nőjön, ha az összes korábbi csúccsal szomszédos új csúcs kerül a gráfba, végül hogy egy klikk-szeparátor két oldalán lévő részgráfok értékei közül a nagyobbikat vegye fel. Az összes ilyen függvény halmaza az elemenkénti minimalizáció és maximalizáció műveleteire nézve teljes hálót alkot. A háló legkisebb eleme a Hadwiger-szám, legnagyobbik pedig a favastagság.

Fordítás

• Ez a szócikk részben vagy egészben a Hadwiger number című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

• Alon, Noga; Lingas, Andrzej & Wahlen, Martin (2007), "Approximating the maximum clique minor and some subgraph homeomorphism problems", Theoretical Computer Science 374 (1–3): 149–158, doi:10.1016/j.tcs.2006.12.021, <http://www.math.tau.ac.il/~nogaa/PDFS/lingas7.pdf>.
• Bollobás, B.; Catlin, P. A. & Erdős, Paul (1980), "Hadwiger's conjecture is true for almost every graph", European Journal of Combinatorics 1: 195–199, doi:10.1016/s0195-6698(80)80001-1, <http://www.renyi.hu/~p_erdos/1980-10.pdf>.
• Eppstein, David (2009), "Finding large clique minors is hard", Journal of Graph Algorithms and Applications 13 (2): 197–204, DOI 10.7155/jgaa.00183.
• Fomin, Fedor V.; Oum, Sang-il & Thilikos, Dimitrios M. (2010), "Rank-width and tree-width of H-minor-free graphs", European Journal of Combinatorics 31 (7): 1617–1628, DOI 10.1016/j.ejc.2010.05.003.
• Hadwiger, Hugo (1943), "Über eine Klassifikation der Streckenkomplexe", Vierteljschr. Naturforsch. Ges. Zürich 88: 133–143.
• Halin, Rudolf (1976), "S-functions for graphs", J. Geometry 8 (1-2): 171–186, DOI 10.1007/BF01917434.
• Kostochka, A. V. (1984), "Lower bound of the Hadwiger number of graphs by their average degree", Combinatorica 4 (4): 307–316, DOI 10.1007/BF02579141.
• Robertson, Neil; Seymour, Paul & Thomas, Robin (1991), "Excluding infinite minors", Discrete Mathematics 95 (1-3): 303–319, DOI 10.1016/0012-365X(91)90343-Z.
• Robertson, Neil; Seymour, Paul & Thomas, Robin (1993a), "Hadwiger's conjecture for K₆-free graphs", Combinatorica 13 (3): 279–361, doi:10.1007/BF01202354, <http://www.math.gatech.edu/~thomas/PAP/hadwiger.pdf>. Hozzáférés ideje: 2018-12-02.
• Robertson, Neil; Seymour, P. D. & Thomas, Robin (1993b), "Linkless embeddings of graphs in 3-space", Bulletin of the American Mathematical Society 28 (1): 84–89, DOI 10.1090/S0273-0979-1993-00335-5.
• Thomason, Andrew (2001), "The extremal function for complete minors", Journal of Combinatorial Theory, Series B 81 (2): 318–338, DOI 10.1006/jctb.2000.2013.
• Wagner, K. (1937), "Über eine Eigenschaft der ebenen Komplexe", Math. Ann. 114: 570–590, DOI 10.1007/BF01594196.