Split gráf
A matematika, azon belül a gráfelmélet területén egy split gráf, hasított gráf vagy kettéhasadó gráf (split graph) olyan gráf, melynek csúcsai egy klikkbe (teljes részgráfba) és egy független csúcshalmazba particionálhatók. Elsőként Földes and Hammer (1977a, 1977b) tanulmányozta őket, tőlük függetlenül Tyshkevich and Chernyak (1979) is bevezette a fogalmat.[1]
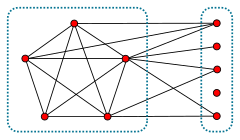
Egy split gráfnak lehet egynél több lehetséges klikkre és független halmazra való particionálása is; például az a–b–c útgráf egy split gráf, melynek csúcsai háromféleképpen particionálhatók:
- az {a,b} klikk és a {c}
- a {b,c} klikk és az {a} független halmaz
- a {b} klikk és az {a,c} független halmaz
A split gráfok tiltott részgráfjaik alapján jellemezhetők: egy gráf pontosan akkor split gráf, ha egyetlen feszített részgráfja sem 4 vagy 5 csúcsú kör, vagy diszjunkt élpár (ami a 4-kör komplementere).[2]
Más gráfcsaládokkal való kapcsolata
szerkesztésA definíció alapján a split gráfok nyilvánvalóan zártak a komplementerképzés műveletére nézve.[3] Egy másik karakterizáció szerint a split gráfok azok a merev körű gráfok, melyek komplementere is merev körű.[4] Ahogy a merev körű gráfok a fák al-fáinak metszetgráfjai, ugyanígy a split gráfok csillaggráfok al-csillagjainak metszetgráfjai.[5] Csaknem minden merev körű gráf splitgráf; ahogy n tart végtelenhez, az n-csúcsú merev körű gráfok között a split gráfok aránya egyhez tart.[6]
Mivel a merev körű gráfok perfektek, ezért a split gráfok is azok. A dupla split gráfok[7] családjának tagjait split gráfokból lehet előállítani minden csúcs megduplázásával (így a klikk antipárosítást feszít ki, a független csúcshalmaz pedig párosítást); a dupla split gráfok a perfekt gráfok öt alaposztályának egyike, melyekből az összes többi perfekt gráf előállítható, ahogy az megjelenik (Chudnovsky et al. 2006) erős perfektgráf-tétel-bizonyításában.
Ha egy gráf egyszerre split és intervallumgráf, akkor komplementere egyszerre split és összehasonlíthatósági gráf, ugyanez igaz megfordítva. A split összehasonlíthatósági gráfok és így a split intervallumgráfok ezért jellemezhetőek három tiltott feszített részgráfjukkal.[8] A split kográfok pontosan megegyeznek a küszöbgráfokkal, a split permutációgráfok pedig pontosan azok az intervallumgráfok, melyek komplementerei is intervallumgráfok.[9] A split gráfok komplementer kromatikus száma 2.
Algoritmikus problémák
szerkesztésTekintsük a G split gráfot, melynek létezik egy C klikkbe és I független csúcshalmazba particionálása. Ekkor a split gráf minden maximális klikkje vagy C-vel egyezik meg, vagy egy I-beli csúcs szomszédságával. Ezért a split gráfokban könnyű feladat meghatározni a maximális klikket, illetve komplementer feladatként a maximális független halmazt. Tetszőleges split gráfban a következő három lehetőség valamelyikének igaznak kell lennie:[10]
- Létezik olyan x csúcs I-ben, hogy C ∪ {x} teljes. Ebben az esetben C ∪ {x} egy maximális klikk, I pedig maximális független halmaz.
- Létezik x csúcs C-ben, hogy I ∪ {x} független. Ebben az esetben I ∪ {x} maximális független halmaz és C maximális klikk.
- C maximális klikk és I maximális független halmaz. Ebben az esetben G-nek a (C,I) klikkre és független halmazra felbontása egyedi, C a maximális klikk és I a maximális független halmaz.
Néhány optimalizálási probléma, ami általánosabb gráfcsaládokon NP-teljes – köztük a gráfszínezés – hasonlóan egyszerűsödik split gráfokat tekintve. A Hamilton-kör keresése továbbra is NP-teljes, még olyan split gráfokra is, melyek erősen merev körűek.[11] Ismert továbbá, hogy a minimális domináló csúcshalmaz problémája split gráfokra is NP-teljes.[12]
Fokszámsorozatok
szerkesztésA split gráfok figyelemre méltó sajátossága, hogy pusztán a gráf fokszámsorozata alapján felismerhetők. Legyen a G gráf fokszámsorozata d1 ≥ d2 ≥ ... ≥ dn, és m a legnagyobb i érték, amire di ≥ i − 1. Ekkor G pontosan akkor split gráf, ha
Ha ez az eset áll fenn, akkor a legnagyobb fokszámú m csúcs maximális klikket alkot G-ben, a maradék csúcsok pedig független csúcshalmazt.[13]
Split gráfok leszámlálása
szerkesztés(Royle 2000) megmutatta, hogy az n-csúcsú split gráfok és bizonyos Sperner-rendszerek között bijekció létesíthető. Ezt a tényt kihasználva meghatározta az n csúcsú (nem izomorf) split gráfok számát. Kis n értékekre, n = 1-től kezdve, ezek:
Ezt a gráfleszámlálási eredményt korábban (Tyshkevich & Chernyak 1990) is bizonyította.
Fordítás
szerkesztés- Ez a szócikk részben vagy egészben a Split graph című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek
szerkesztés- ↑ (Földes & Hammer 1977a) általánosabb definíciója szerint a split gráfoknak nevezett gráfok közé tartoznak a páros gráfok is (tehát a két független csúcshalmazba particionálható gráfok), továbbá a páros gráfok komplementerei (tehát a két klikkbe particionálható gráfok) is. (Földes & Hammer 1977b) az itteni definíciót használja, amit a későbbi irodalom is követ, például: (Brandstädt, Le & Spinrad 1999), Definition 3.2.3, p.41.
- ↑ (Földes & Hammer 1977a); (Golumbic 1980), Theorem 6.3, p. 151.
- ↑ (Golumbic 1980), Theorem 6.1, p. 150.
- ↑ (Földes & Hammer 1977a); (Golumbic 1980), Theorem 6.3, p. 151; (Brandstädt, Le & Spinrad 1999), Theorem 3.2.3, p. 41.
- ↑ (McMorris & Shier 1983); (Voss 1985); (Brandstädt, Le & Spinrad 1999), Theorem 4.4.2, p. 52.
- ↑ (Bender, Richmond & Wormald 1985).
- ↑ Lovásznál[halott link] „kettőzött kettéhasadó gráfok”
- ↑ (Földes & Hammer 1977b); (Golumbic 1980), Theorem 9.7, page 212.
- ↑ (Brandstädt, Le & Spinrad 1999), Corollary 7.1.1, p. 106, and Theorem 7.1.2, p. 107.
- ↑ (Hammer & Simeone 1981); (Golumbic 1980), Theorem 6.2, p. 150.
- ↑ (Müller 1996)
- ↑ (Bertossi 1984)
- ↑ (Hammer & Simeone 1981); (Tyshkevich 1980); (Tyshkevich, Melnikow & Kotov 1981); (Golumbic 1980), Theorem 6.7 and Corollary 6.8, p. 154; (Brandstädt, Le & Spinrad 1999), Theorem 13.3.2, p. 203. (Merris 2003) tovább vizsgálja a split gráfok fokszámsorozatait.
- Bender, E. A.; Richmond, L. B. & Wormald, N. C. (1985), "Almost all chordal graphs split", J. Austral. Math. Soc., A 38 (2): 214–221, DOI 10.1017/S1446788700023077.
- Bertossi, Alan A. (1984), "Dominating sets for split and bipartite graphs", Information Processing Letters 19: 37–40, DOI 10.1016/0020-0190(84)90126-1.
- Brandstädt, Andreas; Le, Van Bang & Spinrad, Jeremy (1999), Graph Classes: A Survey, SIAM Monographs on Discrete Mathematics and Applications, ISBN 0-89871-432-X.
- Chudnovsky, Maria; Robertson, Neil & Seymour, Paul et al. (2006), "The strong perfect graph theorem", Annals of Mathematics 164 (1): 51–229, DOI 10.4007/annals.2006.164.51.
- Földes, Stéphane & Hammer, Peter Ladislaw (1977a), "Split graphs", Proceedings of the Eighth Southeastern Conference on Combinatorics, Graph Theory and Computing (Louisiana State Univ., Baton Rouge, La., 1977), vol. XIX, Congressus Numerantium, Winnipeg: Utilitas Math., pp. 311–315.
- Földes, Stéphane & Hammer, Peter Ladislaw (1977b), "Split graphs having Dilworth number two", Canadian Journal of Mathematics 29 (3): 666–672, DOI 10.4153/CJM-1977-069-1.
- Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press, ISBN 0-12-289260-7.
- Hammer, Peter Ladislaw & Simeone, Bruno (1981), "The splittance of a graph", Combinatorica 1 (3): 275–284, DOI 10.1007/BF02579333.
- McMorris, F. R. & Shier, D. R. (1983), "Representing chordal graphs on K1,n", Commentationes Mathematicae Universitatis Carolinae 24: 489–494.
- Merris, Russell (2003), "Split graphs", European Journal of Combinatorics 24 (4): 413–430, DOI 10.1016/S0195-6698(03)00030-1.
- Müller, Haiko (1996), "Hamiltonian Circuits in Chordal Bipartite Graphs", Discrete Mathematics 156: 291–298, DOI 10.1016/0012-365x(95)00057-4.
- Royle, Gordon F. (2000), "Counting set covers and split graphs", Journal of Integer Sequences 3 (2): 00.2.6, <http://www.emis.ams.org/journals/JIS/VOL3/ROYLE/royle.pdf>. Hozzáférés ideje: 2017-05-23 Archiválva 2016. március 3-i dátummal a Wayback Machine-ben.
- Tyshkevich, Regina I. (1980), "[The canonical decomposition of a graph]", Doklady Akademii Nauk SSSR 24: 677–679
- Tyshkevich, Regina I. & Chernyak, A. A. (1979), "Canonical partition of a graph defined by the degrees of its vertices", Isv. Akad. Nauk BSSR, Ser. Fiz.-Mat. Nauk 5: 14–26.
- Tyshkevich, Regina I. & Chernyak, A. A. (1990), Matem. Zametki 48 (6): 98–105, <http://mi.mathnet.ru/eng/mz3413>. Translated as "Yet another method of enumerating unmarked combinatorial objects" (1990), Mathematical notes of the Academy of Sciences of the USSR 48 (6): 1239–1245, doi:10.1007/BF01240267.
- Tyshkevich, Regina I.; Melnikow, O. I. & Kotov, V. M. (1981), "On graphs and degree sequences: the canonical decomposition", Kibernetika 6: 5–8.
- Voss, H.-J. (1985), "Note on a paper of McMorris and Shier", Commentationes Mathematicae Universitatis Carolinae 26: 319–322.
Kapcsolódó irodalom
szerkesztés- Martin Charles Golumbic, "Algorithmic Graph Theory and Perfect Graphs" c. könyvének egy teljes fejezete a split gráfokat tárgyalja.