Sűrűségfüggvény
A valószínűségszámításban az X valószínűségi változó sűrűségfüggvénye f pontosan akkor, ha az X-nek az F-fel jelölt eloszlásfüggvénye előállítható a következő alakban:
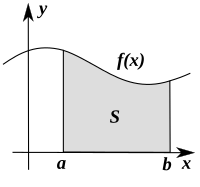
Szemben a valószínűségekkel, a sűrűségfüggvények felvehetnek 1-nél nagyobb értéket is. A valószínűségi eloszlások sűrűségfüggvényeken alapuló konstrukciója szempontjából nem a sűrűségfüggvény által felvett érték a fontos, hanem az integrál.
A sűrűségfüggvény általánosítása az általánosított sűrűségfüggvény, ahol is a Lebesgue-mértékre vonatkozó sűrűségfüggvények a valószínűségi sűrűségfüggvények. A továbbiakban sűrűségfüggvényen valószínűségi sűrűségfüggvényt értünk, kivéve ha azt máshogy jelezzük.
Diszkrét esetben az események valószínűsége megkapható a tartalmazott elemi események valószínűségeinek összegzésével. Folytonos esetben azonban ez nem tehető meg, mivel a nullaszor végtelen értéke bármi lehet. Például két ember csak ritkán pont egyforma magas, eltér egymástól egy hajszállal vagy csak néhány atomnyival. A sűrűségfüggvénnyel tetszőleges intervallum valószínűsége meghatározható, így a nullaszor végtelen probléma megkerülhető.
Definíció
szerkesztésA sűrűségfüggvény definiálható valószínűségeloszlás alapján, vagy pedig a valószínűségeloszlást lehet levezetni a sűrűségfüggvényből.
Az önálló definícióban szerepel az tulajdonság, a nemnegativitás, az integrálhatóság és a normáltság, azaz a teljes -en vett integrál egy. Ekkor definiálható hozzá
- valószínűségeloszlás.
Megfordítva, levezethető valószínűségi mértékből. Ekkor, ha az függvényre minden esetén
illetve
akkor sűrűségfüggvény.
Tulajdonságai
szerkesztésLétezés
szerkesztés- Diszkrét eloszlású valószínűségi változóknak nincs sűrűségfüggvénye.
- Sűrűségfüggvénye csak folytonos eloszlású valószínűségi változónak lehet.
- Még a folytonos eloszlású valószínűségi változók közül sincs mindnek sűrűségfüggvénye, csak egy speciális osztályuknak, az abszolút folytonos valószínűségi változóknak, melyeket pontosan azzal a tulajdonsággal definiálunk, hogy van sűrűségfüggvényük.
Általános tulajdonságok
szerkesztés- A definícióból nyilvánvalóan látszik, hogy
- bármely sűrűségfüggvény esetén. Ám az is megmutatható, hogy egy tetszőleges f mérhető függvény pontosan akkor sűrűségfüggvény (vagyis pontosan akkor található hozzá olyan valószínűségi változó, melynek sűrűségfüggvénye) ha f(x) ≥ 0 majdnem mindenütt és a fenti tulajdonság teljesül rá.
- A sűrűségfüggvény ismeretében több, a valószínűségi változóval kapcsolatos esemény valószínűsége megadható. Bármely A Borel-halmaz esetén
- Speciálisan
a két definíció egyenértékű.
Kapcsolat az eloszlásfüggvénnyel
szerkesztésHa az eloszlásfüggvény folytonos, és legfeljebb megszámlálható végtelen pontban nem differenciálható, akkor van sűrűségfüggvénye, és:
Más jelöléssel, F '(x)=f(x), vagyis az eloszlásfüggvényből egyszerű deriválással kapjuk a sűrűségfüggvényt.
Vannak olyan eloszlások, mint a Cantor-eloszlás, amelyek eloszlásfüggvénye folytonos, és majdnem mindenütt differenciálható, de nincs sűrűségfüggvényük. A folytonos eloszlások eloszlásfüggvénye majdnem mindenütt differenciálható, de a derivált csak az abszolút folytonos részt foglalja magába.
Megfordítva, a sűrűségfüggvényből is kiszámítható az eloszlásfüggvény (abszolút folytonos) része:
ami azonnal következik a definícióból.
Sűrűségfüggvény részintervallumon
szerkesztésHa egy valószínűségi változó csak egy részintervallumból vesz fel elemeket, akkor a sűrűségfüggvény választható úgy, hogy az intervallumon kívül a 0 értéket veszi fel. Erre példa az exponenciális eloszlás, ahol . Egy alternatív lehetőség az értelmezési tartomány leszűkítése, azaz definiálása. Ekkor az eloszlás sűrűségét az intervallumon adja meg a Lebesgue-mérték szerint.
Nemlineáris transzformáció
szerkesztésA nemlineáris transzformáció esetén
- .
Konvolúció
szerkesztésAbszolút folytonos eloszlás esetén a valószínűségeloszlások konvolúciója visszavezethető a sűrűségfüggvények konvolúciójára. Ha abszolút folytonos eloszlások az és eloszlásfüggvényekkel, akkor : .
Itt a és konvolúciója, és az és konvolúciója. Tehát a konvolúció és a sűrűségfüggvény képzése felcserélhető.
Ez a tulajdonság közvetlenül átvihető független valószínűségi változók összegére. Legyenek valószínűségi változók az és sűrűségfüggvényekkel, ekkor
- .
Tehát az összeg sűrűségfüggvénye megegyezik a tagok sűrűségfüggvényeinek konvolúciójával.
Példák
szerkesztésAz exponenciális eloszlás abszolút folytonos eloszlás, sűrűségfüggvénye
ahol valós paraméter. Ha , akkor az helyen 1-nél nagyobb értéket vesz fel. Az, hogy sűrűségfüggvény, adódik az exponenciális függvény elemi integrációs szabályából, a nemnegativitás közvetlenül következik a hatványozás szabályaiból, és az integrálhatóság is bizonyítható.
A véges intervallumon egyenletes eloszlásnak is van sűrűségfüggvénye, például a intervallumon. Az általa megadott valószínűség
- , ha és
Az intervallumon kívüli események valószínűsége nulla. Az sűrűségfüggvény megfelel az
feltételeknek. Az alkalmas függvény, amit a intervallumon kívül nulla folytat az integrálhatóság kedvéért. Ezzel a folytonos egyenletes eloszlás sűrűségfüggvénye:
Egy másik megfelelő függvény:
A két függvény egy Lebesgue-nullmértékű halmazon különbözik csak, és mindkettő megfelel a követelményeknek. Mivel egy tetszőleges pontban meg lehet változtatni az értéket, azért egy valószínűségeloszlásnak legalább kontinuum sok sűrűségfüggvénye van. Az integrálok értéke nem változik, tehát a módosított sűrűségfüggvény is sűrűségfüggvény marad.
Megjegyzések a definícióhoz
szerkesztésSzigorúan véve a definícióban egy Lebesgue-mérték szerinti integrál szerepel, amit úgy kellene jelölni, hogy . Többnyire azonban a Riemann-integrál is megfelel, emiatt szoktak a definícióban integrált írni. A különbséget az jelenti, hogy a Riemann-integrálnak nincs mértékelméleti háttere, míg a Lebesgue-integrálnak van.
A német szakirodalom meg is különbözteti a két eljárást. Amiből a valószínűségeloszlást származtatják, az a Wahrscheinlichkeitsdichte, a másik a Verteilungsdichte.[1]
Létezés és egyértelműség
szerkesztésValószínűségeloszlásból származtatva
szerkesztésA valószínűségeloszlással definiált esetben a valószínűségi mértékből származik a valószínűségeloszlás. A normáltságból következik . Mivel a valószínűségek nem lehetnek negatívak, a függvény sehol se negatív. a σ-additív tulajdonság következik a majorált konvergencia tételéből, a sűrűségfüggvénnyel mint majoránssal és az
függvénysorozattal, ahol az halmazok páronként diszjunktak, és az halmaz karakterisztikus függvénye.
Az egyértelműség következik a mérték egyértelműségének tételéből, és a Borel-σ-algebra generátorainak metszetstabil tulajdonságából, ami itt a zárt intervallumok.
A másik definíció alapján
szerkesztésA Radon-Nikodým-tétellel belátható, hogy adott valószínűségeloszláshoz létezik sűrűségfüggvény:
- Ha valószínűségeloszlás, akkor akkor és csak akkor van sűrűségfüggvénye, ha abszolút folytonos a Lebesgue-mértékre. Ez azt jelenti, hogy ha , akkor .
Ez nem zárja ki, hogy több sűrűségfüggvény létezik, de mindegyik csak Lebesgue-nullmértékű halmazon különbözik a többitől, azaz majdnem mindenütt egyenlőek.
Emiatt a diszkrét valószínűségeloszlásoknak nincs sűrűségfüggvénye, mivel egy alkalmas elemre mindig teljesül, hogy . Ezeknek a ponthalmazoknak azonban a Lebesgue-mértéke nulla, vagyis a diszkrét valószínűségeloszlások nem abszolút folytonosak.
A valószínűségek számítása
szerkesztésAlapok
szerkesztésAdva legyen az sűrűségfüggvény, ekkor az intervallum valószínűsége
- .
Itt mindegy, hogy az intervallum zárt-e, vagy nyílt, félig nyílt, mivel a folytonos valószínűségi változók esetén egy pont valószínűsége nulla. Formálisan,
Bonyolultabb halmazok esetén az egyes intervallumokon vett integrálokat kell összeadni. Ekkor a képlet
- .
Alkalmazható a σ-additivitás is, ami azt jelenti, hogy a páronként diszjunkt intervallumok, és
az összes egyesítése, akkor
- .
ahol . Ez érvényes véges sok és végtelen számú intervallumra. Diszjunkt intervallumok valószínűsége összeadódik.
Példa
szerkesztésEgy callcenterben két hívás között eltelt idő megközelítően exponenciális eloszlású. Legyen ennek paramétere ! Ekkor a sűrűségfüggvény
- .
Az x tengely beosztását a paraméter határozza meg úgy, hogy idő alatt várható értékben egy hívás fut be. Annak a valószínűsége, hogy a következő hívás egy és két időegység után következik be:
- .
Tegyük fel, hogy egy munkatárs öt időegység hosszú szünetet tart! Annak a valószínűsége, hogy közben nem érkezik hívás, egyenlő azzal a valószínűséggel, hogy a következő hívásig öt vagy több időegység telik el. Ennek valószínűsége
Jellemző számadatok meghatározása
szerkesztésEgy valószínűségi változó jellemző számadatai közül több is megadható a valószínűségi változó sűrűségfüggvényének segítségével.
Módusz
szerkesztésEgy valószínűségeloszlás illetve valószínűségi változó módusza definiálható a sűrűségfüggvénnyel: Ahol a sűrűségfüggvénynek maximuma van, ott van a módusz. Formálisan, akkor módusza az sűrűségfüggvényű valószínűségi változónak, ha az hely lokális maximumhely.[2] ez azt jelenti, hogy
- van , hogy minden helyen.
Egy sűrűségfüggvénynek több lokális maximumhelye is lehet, ekkor az eloszlás bimodális vagy multimodális. Az egyenletes eloszlás esetén minden hely módusz.
Medián
szerkesztésA mediánt rendszerint az eloszlásfüggvénnyel és kvantilisekkel definiálják. Abszolút folytonos eloszlás mediánja számítható sűrűségfüggvénnyel: az eloszlás vagy a valószínűségi változó mediánja, ha:
és
Folytonosság miatt mindig létezik, de az egyértelműség nem garantált, például csak két diszjunkt intervallum unióján nullától különböző értékeket felvevő szimmetrikus sűrűségfüggvény esetén.
Várható érték
szerkesztésHa az valószínűségi változó sűrűségfüggvénye , akkor várható értéke:
- ,
ha az integrál konvergens. Ha nem konvergens, akkor a valószínűségi változónak nincs várható értéke.
Szórásnégyzet és szórás
szerkesztésHa az valószínűségi változó sűrűségfüggvénye , és várható értéke , akkor szórásnégyzete
- .
Vagy az eltolási tétellel:
- .
Ezek a képletek csak akkor használhatók, ha az integrálok konvergensek. A szórás a szórásnégyzetből számítható gyökvonással, de sokszor elég a szórásnégyzetet használni.
Magasabb momentumok, ferdeség és lapultság
szerkesztésA fent leírt nemlineáris transzformáció felhasználásával közvetlenül kiszámíthatók a további momentumok. Így ha az valószínűségi változó sűrűségfüggvénye , akkor:
és a k-adik abszolút momentum
- .
Ha várható értéke , akkor a centrális momentumok:
és az abszolút centrális momentumok:
- .
Példa
szerkesztésPéldaként tekintsük az exponenciális eloszlást:
ahol paraméter!
Az exponenciális eloszlásnak mindig módusza a nulla. A intervallumon a sűrűségfüggvény konstans nulla, és az intervallumon szigorúan monoton csökken, így a 0 helyen lokális maximum van. A monotóniából következik, hogy nincs több lokális maximum, a módusz egyértelmű.
A centrális momentumokból meghatározható a ferdeség és a lapultság.
A medián meghatározásához elég a félegyenesen integrálni, mivel a negatív számokon a függvény értéke konstans nulla:
- .
Rövid számolással
- .
Ez teljesíti a mediánra vonatkozó második egyenlőséget is, tehát valóban medián.
A várható érték meghatározható parciális integrállal:
- .
A parciális integrál kétszeri alkalmazásával számítható a szórásnégyzet is.
További példák
szerkesztésLegyen most az sűrűségfüggvény , ha ; ha ; és ha ! Ekkor valóban sűrűségfüggvény, mivel nemnegatív teljes -en, továbbá
- .
Minden esetén:
Az eloszlásfüggvény
Ha valószínűségi változó, aminek sűrűségfüggvénye , akkor például
- .
Az változó várható értéke
- .
Többdimenziós sűrűségfüggvény
szerkesztésTöbbdimenziós valószínűségi változókra is definiálható sűrűségfüggvény, ha eloszlásuk abszolút folytonos. Legyen az valószínűségi vektorváltozó értékű; ekkor az (Lebesgue-mérték szerinti) sűrűségfüggvénye, ha
minden Borel-halmazra.
Speciálisan, az dimenziós intervallumokra, ahol valós számok:
- .
Valószínűségi vektorváltozóknak is definiálható eloszlásfüggvény. Itt , ahol az egyenlőtlenség komponensenként értendő. Ekkor az teret a [0,1] intervallumra képezi úgy, hogy
- .
Ha n-szer folytonosan differenciálható, akkor a sűrűségfüggvény parciális differenciálással megkapható:
Az komponensek sűrűségfüggvényei a peremeloszlások többi komponens szerinti integrálásával kaphatók.
Továbbá: Ha értékű sűrűségfüggvényes valószínűségi vektorváltozó, akkor a következők ekvivalensek:
- Az sűrűségfüggvényének alakja , ahol az sűrűsége.
- Az valószínűségi változók függetlenek.
Becslés diszkrét adatok alapján
szerkesztésFolytonosnak tekintett eloszlásból származó, de diszkréten mért adatok, például testmagasság centiméterben mérve reprezentálhatók gyakorisági sűrűségfüggvényként. Magsűrűségbecslőkkel a sűrűségfüggvény folytonos függvénnyel becsülhető. Az ehhez használt magnak a mérési hibához kell alkalmazkodnia.
Legyen approximáló véletlen változó, az jellemző mennyiségekkel és valószínűségekkel. Az diszkrét approximáló valószínűségi változó határátmenete az folytonos valószínűségi változóba valószínűségi hisztogrammal modellezhető. Ehhez lehetséges értékeit a szakaszokra osztujk fel. Ezek a hosszú intervallumok és a hozzájuk tartozó osztályközepek a sűrűségfüggvény approximációját szolgálják, szemléletesen a valószínűségi hisztogrammal, ami az osztályközepekre emelt téglalapokból áll. Kis esetén felfogható a folytonos valószínűségi változó approximációjaként. Minél rövidebbek a szakaszok, annál jobban közelíti a folytonos valószínűségi változót. Az határátmenet minden intervallumra a következőhöz vezet:[3]
- a szórásnégyzet esetén
- a várható érték esetén
- .
A sűrűségfüggvény általánosítása
szerkesztésLétezik a matematikai statisztikában a sűrűségfüggvénynek egy általánosítása, az általánosított sűrűségfüggvény, mely a valószínűségi mező egy általánosításán, a statisztikai mezőn értelmezett, s definíciójában olyan mély mértékelméleti eszközöket használ, mint a Radon–Nikodym-derivált. Általánosított sűrűségfüggvénye minden valószínűségi változónak van, s abszolút folytonos esetben a sűrűségfüggvénnyel, míg diszkrét esetben a P függvénnyel azonos.
Jegyzetek
szerkesztésForrások
szerkesztés- Bognár J.-né – Mogyoródi J. – Prékopa A. – Rényi A. – Szász D. (2001): Valószínűségszámítási feladatgyűjtemény. Typotex Kiadó, Budapest.
- Fazekas I. (szerk.) (2000): Bevezetés a matematikai statisztikába. Kossuth Egyetemi Kiadó, Debrecen.
- Lukács O. (2002): Matematikai statisztika. Műszaki Könyvkiadó, Budapest.
- Hans-Otto Georgii: Stochastik: Einführung in die Wahrscheinlichkeitstheorie und Statistik. 4. Auflage. de Gruyter Lehrbuch, Berlin 2009, ISBN 978-3-11-021526-7.
- Norbert Henze: Stochastik für Einsteiger. 7. Auflage. Vieweg Verlag, Wiesbaden 2008, ISBN 978-3-8348-0423-5.
- Achim Klenke: Wahrscheinlichkeitstheorie. 2. Auflage. Springer-Verlag, ISBN 978-3-540-76317-8.
- Lothar Sachs, Jürgen Hedderich: Angewandte Statistik: Methodensammlung mit R. 12. Auflage. Springer-Verlag, Berlin / Heidelberg 2006, ISBN 978-3-540-32160-6.
- N.G. Ushakov: Density of a probability distribution
- Weisstein, Eric W.: Probability Density Function (angol nyelven). Wolfram MathWorld
Fordítás
szerkesztésEz a szócikk részben vagy egészben a Wahrscheinlichkeitsdichtefunktion című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.


