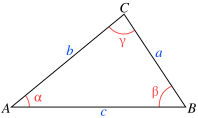
A tangenstétel egy geometriai tétel, miszerint egy tetszőleges háromszög két oldalára és az oldalakkal szemben fekvő szögekre igaz a következő összefüggés:
Háromszög esetén, α , β és γ jelöli az a , b és c oldalakkal szemközti szögeket
a
+
b
a
−
b
=
t
g
α
+
β
2
t
g
α
−
β
2
.
{\displaystyle {\frac {a+b}{a-b}}\ =\ {\frac {\mathrm {tg} {\frac {\alpha +\beta }{2}}}{\mathrm {tg} {\frac {\alpha -\beta }{2}}}}.}
A szinusztétel értelmében:
a
sin
α
=
b
sin
β
.
{\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}.}
Legyen
d
=
a
sin
α
=
b
sin
β
,
{\displaystyle d={\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }},}
így
a
=
d
sin
α
és
b
=
d
sin
β
,
{\displaystyle a=d\sin \alpha {\text{ és }}b=d\sin \beta ,}
amiből
a
+
b
a
−
b
=
d
sin
α
+
d
sin
β
d
sin
α
−
d
sin
β
=
sin
α
+
sin
β
sin
α
−
sin
β
.
{\displaystyle {\frac {a+b}{a-b}}={\frac {d\sin \alpha +d\sin \beta }{d\sin \alpha -d\sin \beta }}={\frac {\sin \alpha +\sin \beta }{\sin \alpha -\sin \beta }}.}
A két szinusz összegére vonatkozó képlet
sin
α
±
sin
β
=
2
sin
(
α
±
β
2
)
cos
(
α
∓
β
2
)
{\displaystyle \sin \alpha \pm \sin \beta =2\sin \left({\frac {\alpha \pm \beta }{2}}\right)\cos \left({\frac {\alpha \mp \beta }{2}}\right)\;}
használatával a következő alakot kapjuk:
a
+
b
a
−
b
=
2
sin
α
+
β
2
cos
α
−
β
2
2
sin
α
−
β
2
cos
α
+
β
2
=
t
g
α
+
β
2
t
g
α
−
β
2
.
{\displaystyle {\frac {a+b}{a-b}}={\frac {2\sin {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}}{2\sin {\frac {\alpha -\beta }{2}}\cos {\frac {\alpha +\beta }{2}}}}=\ {\frac {\mathrm {tg} {\frac {\alpha +\beta }{2}}}{\mathrm {tg} {\frac {\alpha -\beta }{2}}}}.}
Ezzel a tételt bebizonyítottuk.